在完成网络模型的创建、几何参数的赋予、相创建和物理模型建立(在OpenPNM V3中Geometry和Physics模块被移除,相关功能被拆分至Network和Phase模块里)之后就是定义算法和边界条件
OpenPNM V2简易教程可参考:https://zhuanlan.zhihu.com/p/488306648
在V3版本中除了体积流率需要额外计算外,创建几何和物理模型都可以直接通过add_model添加预定义的模型
这里通过几个算例来演示关于算法和边界条件的相关操作
模拟单相流
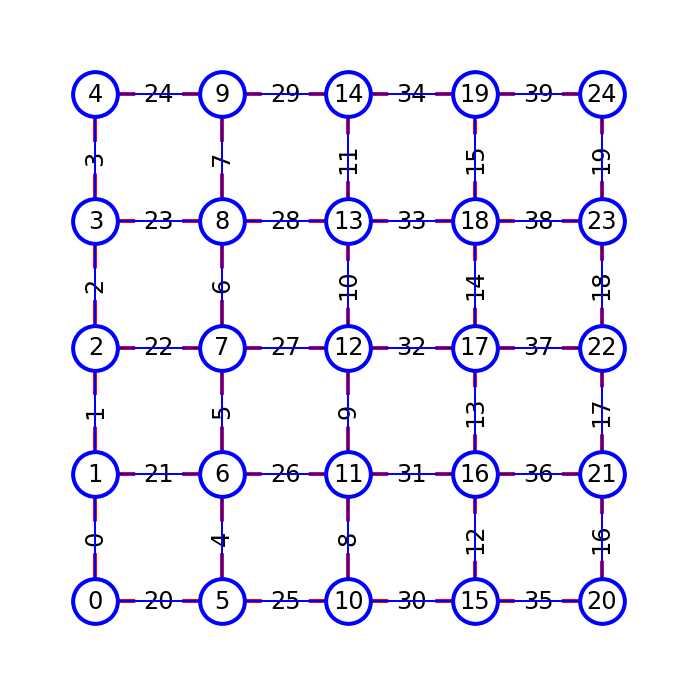
创建网络模型
首先,创建网络信息,这里采用包含了几何信息的立方网络:Demo
import numpy as np
import openpnm as op
import matplotlib.pyplot as plt
op.visualization.set_mpl_style()
pn = op.network.Demo(shape=[5, 5, 1], spacing=5e-5)
ax = op.visualization.plot_connections(pn)
ax = op.visualization.plot_coordinates(pn, ax=ax)
op.visualization.plot_tutorial(pn)
print(pn)
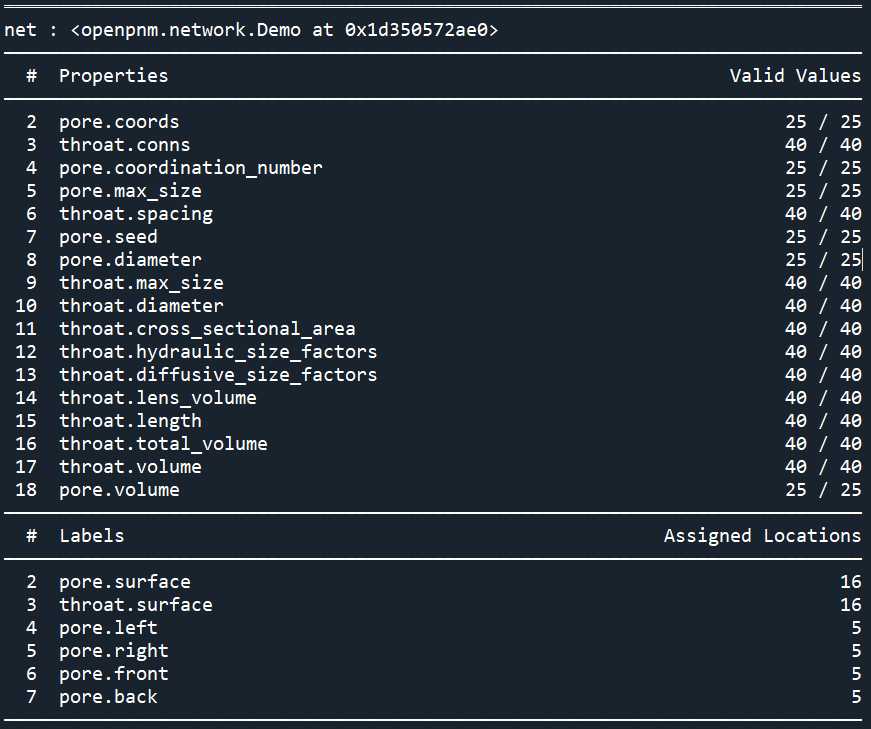
创建相
然后,创建相,这里以最常见的水为例:
water = op.phase.Phase(network=pn)
#添加一个孔隙尺度模型来计算水的粘度:
water.add_model(propname='pore.viscosity',
model=op.models.phase.viscosity.water_correlation)
print(water)
print(water['pore.viscosity'])
'''
[0.00089319 0.00089319 0.00089319 0.00089319 0.00089319 0.00089319
0.00089319 0.00089319 0.00089319 0.00089319 0.00089319 0.00089319
0.00089319 0.00089319 0.00089319 0.00089319 0.00089319 0.00089319
0.00089319 0.00089319 0.00089319 0.00089319 0.00089319 0.00089319
0.00089319]
'''
计算体积流率
简单的算法
假设最简单的情况,即所有压力损失都发生在喉咙中。
流经圆柱形管体积流率是通过Hagan-Poiseuille方程来计算
$ Q=pi*R^4\Delta P/8\mu L $
$\Delta P 是压力损失$
$L 是细管长度$
$\mu 是黏度$
$Q 是体积流率$
$R 是半径$
$g_h=pi*R^4/8\mu L 称为水力传导系数,又称渗透系数$
现在让我们计算渗透系数:
R = pn['throat.diameter']/2
L = pn['throat.length']
mu = water['throat.viscosity'] # See ProTip below
water['throat.hydraulic_conductance'] = np.pi*R**4/(8*mu*L)
print(water['throat.hydraulic_conductance'])
'''
[5.49820616e-15 9.99180736e-15 1.76321626e-14 5.07941658e-14
1.64674238e-14 1.56232587e-14 1.96205099e-14 3.29420230e-14
2.68272625e-15 2.41058903e-15 1.29513705e-15 1.37408974e-15
1.32009256e-15 1.26713904e-15 4.42946704e-15 3.66379252e-14
2.80882220e-14 1.85490397e-15 2.03568403e-15 8.86119497e-14
6.09330649e-15 9.96513487e-15 1.60549434e-14 3.04048800e-14
8.60638597e-14 1.96692761e-14 2.64071141e-15 4.56641017e-15
1.48844528e-15 1.28969372e-14 7.23297734e-15 1.24406579e-15
3.35705479e-15 1.68077772e-15 1.15437363e-14 7.47824866e-15
1.52303130e-15 1.53995733e-15 9.79881973e-14 3.60120595e-14]
'''
孔径和流道半径等几何参数是根据随机种子计算的,每次计算的数值会不一样所以导致体积流率的数值不同,想要使每次计算结果一致,则只需在创建网络模型前添加 np.random.seed(0)即可
water.interpolate_data('throat.viscosity')
water['throat.viscosity']
'''
array([0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319,
0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319,
0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319,
0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319,
0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319,
0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319,
0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319,
0.00089319, 0.00089319, 0.00089319, 0.00089319, 0.00089319])
'''
从上面的代码演示中可以看到,即便water模型里没有throat.viscosity的字典键,我们仍然可以打印出来。
这是因为Phase模型具有将孔隙值插值到流道的特殊能力,反之亦然。
在PNM模拟中,所有的平衡都是围绕每个孔隙求解的,因此热力学性质如温度、压力等都是在孔隙上定义的。因此,物理性质也在孔隙中定义
OpenPNM为此提供了这样一种快捷方式,例如,如果请求一个不存在的流道属性,它将尝试获取孔隙的对应值并对值进行线性插值以生成流道的值数组。
严谨的算法
除了流道内的压力损失外,还因该注意以下三点:
- 考虑每个半孔和流道的渗透率。
- 流道长度应该考虑球形孔体和圆柱形流道之间的重叠部分来仔细计算。
- 孔隙的净截面积是通过孔中心和孔与流道的交点之间的积分来计算的
print(pn)
pn['throat.hydraulic_size_factors']
'''
[[2.74055386e-16 1.79111358e-17 3.27301354e-16]
[3.63255347e-16 2.26972347e-17 3.23512572e-16]
[2.88639845e-16 1.66334187e-17 2.70663772e-16]
[2.08378814e-16 9.05573092e-18 1.79279846e-16]
[2.41047346e-16 1.01860637e-17 1.88532351e-16]
[1.88532351e-16 1.14942402e-17 3.06377616e-16]
[6.91599038e-16 7.94384341e-17 7.33276170e-16]
[2.87560873e-16 8.96086740e-18 1.54282093e-16]
[3.39009315e-16 1.70105711e-17 2.57155332e-16]
[2.57155332e-16 1.52114636e-17 2.68854437e-16]
[2.91059527e-16 2.18393246e-17 4.13171768e-16]
[1.06381806e-16 1.03160463e-18 3.35319054e-17]
[2.79970479e-17 4.67608999e-19 2.38078927e-17]
[2.38078927e-17 6.17285071e-19 7.89928756e-17]
[5.50899795e-16 4.86887382e-17 5.24692673e-16]
[5.24692673e-16 4.98014766e-17 5.69207454e-16]
[6.44601336e-16 5.76268801e-17 5.53255336e-16]
[2.96667276e-16 1.23677349e-17 2.05130578e-16]
[2.05130578e-16 1.22530283e-17 2.91432658e-16]
[1.12444070e-16 1.44145783e-18 4.46657991e-17]
[2.74055386e-16 1.72960370e-17 3.04721477e-16]
[2.59224373e-16 1.05277663e-17 1.88532351e-16]
[3.23512572e-16 2.49701058e-17 4.28471886e-16]
[2.70663772e-16 2.00843657e-17 4.07871557e-16]
[1.62848722e-16 6.95389550e-18 1.54282093e-16]
[3.67078481e-16 2.83494786e-17 4.23444187e-16]
[1.88532351e-16 9.64767948e-18 2.11038523e-16]
[4.01213836e-16 2.14344968e-17 2.91059527e-16]
[7.70450700e-16 8.91544104e-17 7.47360177e-16]
[5.93659807e-17 8.29515339e-19 3.35319054e-17]
[1.01002324e-16 1.11930428e-18 3.70875827e-17]
[5.79797727e-17 5.47276971e-19 2.38078927e-17]
[2.91059527e-16 2.07575126e-17 3.80441333e-16]
[5.96817367e-16 5.15350675e-17 5.24692673e-16]
[3.35319054e-17 1.00672933e-18 1.01549457e-16]
[3.70875827e-17 1.21523141e-18 1.18381191e-16]
[2.38078927e-17 6.08744683e-19 7.66784021e-17]
[3.06100627e-16 1.25785692e-17 2.05130578e-16]
[5.24692673e-16 4.72033285e-17 5.25821568e-16]
[1.21860727e-16 1.49864288e-18 4.46657991e-17]]
'''
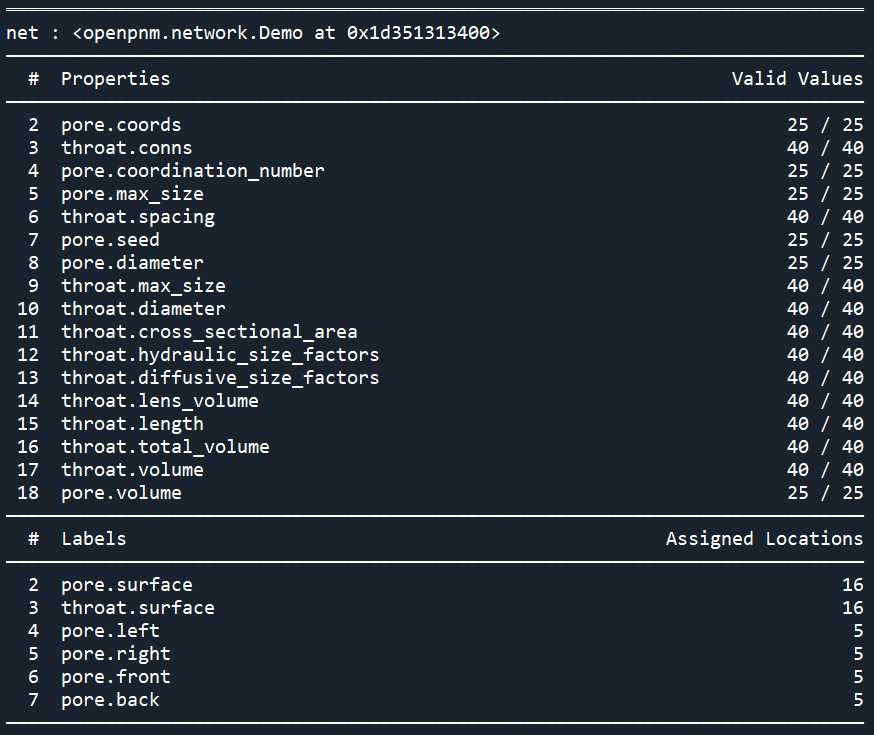
数组throat.hydraulic_size_factors是根据网络上的孔隙尺度模型计算的。在上述的三个注意点上计算的更加严谨
每个流道的水力传导系数是一个Nt-by-3数组,其中第一和第三列是流道两端半孔的水力传导系数,中间一列是流道的渗透系数。
根据Hagan-Poiseuille方程,水力传导系数或者渗透系数是由流体粘度和容器的几何参数决定的,在严谨的算法中流道的渗透系数包括两个半球和一个圆柱体内的渗透系数,所以Hagan-Poiseuille方程可以这样写
$Q=F_h \Delta P /\mu=g_h \Delta P$
$F_h=pi*R^4/8 L$
$Q=\Delta P /(\mu/F_h ,_i+\mu/F_h ,_j+\mu/F_h ,_k)$
F_h = water['throat.hydraulic_size_factors']
water['throat.hydraulic_conductance'] = (mu * (1/F_h).sum(axis=1))**(-1)
print(water['throat.hydraulic_conductance'])
'''
[1.79031699e-14 2.24355192e-14 1.66408558e-14 9.26774109e-15
1.04025141e-14 1.17150032e-14 7.27093840e-14 9.21045492e-15
1.70601726e-14 1.52639504e-14 2.16784149e-14 1.11005046e-15
5.05167063e-16 6.68542806e-16 4.61498082e-14 4.71552966e-14
5.40551328e-14 1.25652687e-14 1.24510347e-14 1.54419931e-15
1.72915552e-14 1.07498356e-14 2.46208856e-14 2.00152770e-14
7.15723217e-15 2.77400028e-14 9.84728144e-15 2.12921344e-14
8.08217352e-14 8.94098524e-16 1.20349374e-15 5.93476871e-16
2.06414110e-14 4.87077477e-14 1.08383083e-15 1.30441885e-15
6.59442665e-16 1.27744646e-14 4.47964989e-14 1.60429524e-15]
'''
#孔隙尺度模型
water.add_model(propname='throat.hydraulic_conductance',
model=op.models.physics.hydraulic_conductance.generic_hydraulic)
print(water['throat.hydraulic_conductance'])
'''
[1.79031699e-14 2.24355192e-14 1.66408558e-14 9.26774109e-15
1.04025141e-14 1.17150032e-14 7.27093840e-14 9.21045492e-15
1.70601726e-14 1.52639504e-14 2.16784149e-14 1.11005046e-15
5.05167063e-16 6.68542806e-16 4.61498082e-14 4.71552966e-14
5.40551328e-14 1.25652687e-14 1.24510347e-14 1.54419931e-15
1.72915552e-14 1.07498356e-14 2.46208856e-14 2.00152770e-14
7.15723217e-15 2.77400028e-14 9.84728144e-15 2.12921344e-14
8.08217352e-14 8.94098524e-16 1.20349374e-15 5.93476871e-16
2.06414110e-14 4.87077477e-14 1.08383083e-15 1.30441885e-15
6.59442665e-16 1.27744646e-14 4.47964989e-14 1.60429524e-15]
'''
创建算法对象
创建一个stokes流动模型
op.algorithms.StokesFlow
sf = op.algorithms.StokesFlow(network=pn, phase=water)
#Definition : StokesFlow(name='stokes_?', *, phase, network)
#A subclass of LinearTransport to simulate viscous flow.
print(sf)
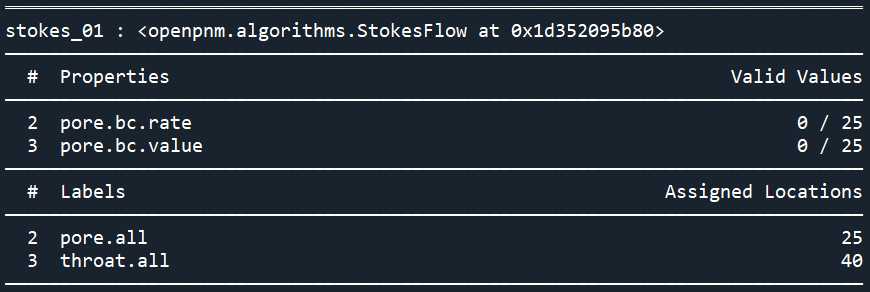
指定边界条件
可以看到算法的属性里包含了边界条件:pore.bc , bc.value表示边界的压力,bc.rate表示边界的流速
边界条件有预定义的数组但没有有效值,所以,现在定义网络左边为压力进口,网络右边为速度出口:
sf.set_value_BC(pores=pn.pores('left'), values=100_000)
sf.set_rate_BC(pores=pn.pores('right'), rates=1e-10)
print(sf)
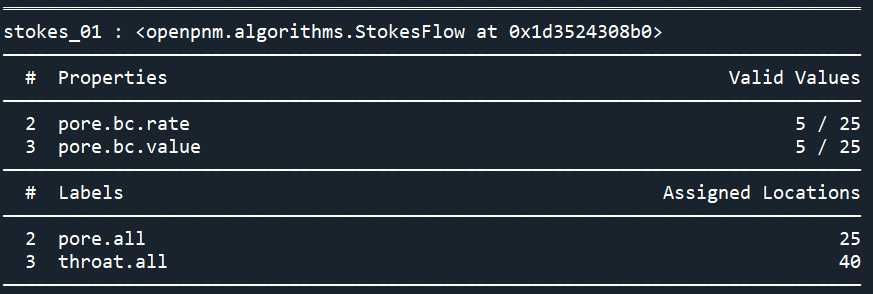
soln = sf.run()#`soln` is a `dict` with the `quantity` as the `key` (i.e. `'pore.pressure'`) and the solution as the `value` (i.e an `ndarray`).
print(soln)
#None
该方法求解了每个孔隙周围的质量平衡,并计算了每个孔隙内维持边界条件所定义的流动所需的压力。最后,我们可以看看指定孔隙中需要多少压力才能满足所需的流速:
ax = op.visualization.plot_connections(pn)
ax = op.visualization.plot_coordinates(pn, ax=ax, color_by=water['pore.pressure'])
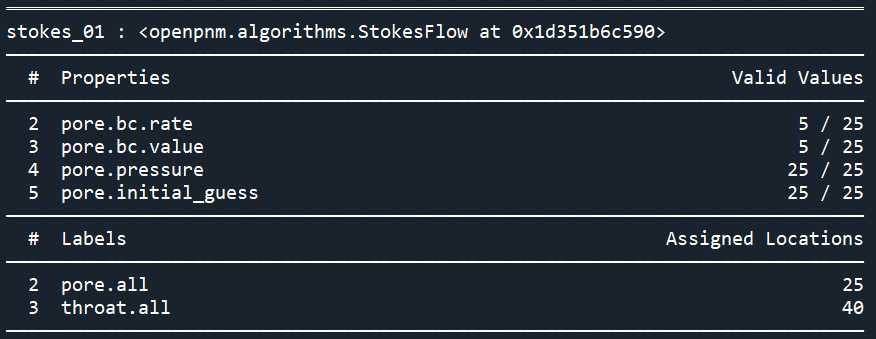
print(sf)
print(sf['pore.pressure'][pn.pores('right')])
'''
[146047.14279219 144668.45513766 131818.50627857 123987.42334449
153492.37334527]
'''





Comments NOTHING