OpenFOAM中的坐标变换

Please refresh the page if equations are not rendered correctly.
---------------------------------------------------------------

有关复合材料的模拟中有时要用到坐标变换，在三维空间中，我们需要设置复合材料局部的面内和层间渗透率，这就需要对渗透率张量进行坐标变换。关于坐标变换，引用李东岳译的OpenFOAM用户指南中的一段话，

2 阶张量可以定义为矢量的线性函数，例如：向量 $a$ 和向量 $b$ 可以通过二阶张量 $T$ 联系起来 $a=T\cdot b$ 。我们可以通过改变 $T$ 中的分量来使 $T$ 能够对张量实现不同的坐标变换，例如从 $x,y,z$ 的坐标系统变换为 $x', y', z'$ 坐标系统。这种变换称之为张量转换。然而，标量在坐标系变换时不发生变化。矢量可实现变换： $a'=T\cdot a$ 。二阶张量 $S$ 可以通过下述公式变换成为 $S'$ : $S'=T \cdot S \cdot T^T$ 。

以下几个简单的算例展示如何在OpenFOAM中快速实现这一过程而避免自己造轮子。

算例1

使用 foamNewApp 命令创建一个名为 zzbh_test 的测试用的求解器。并写入如下的代码，

#include "fvCFD.H"
#include "axesRotation.H"
int main(int argc, char *argv[])
{
    vector e3_local(0,0,1);
    vector e1_local(1,1,0);
    tensor Rz = axesRotation(e3_local, e1_local).R();
    vector local_e1 = axesRotation(e3_local, e1_local).e1();
    vector local_e2 = axesRotation(e3_local, e1_local).e2();
    vector local_e3 = axesRotation(e3_local, e1_local).e3();
    Info << "Rotation matrix Rz: " << Rz << nl;
    Info << "local x-axis: " << local_e1 << nl;
    Info << "local y-axis: " << local_e2 << nl;
    Info << "local z-axis: " << local_e3 << nl;
    return 0;
}

wmake编译后即可运行。输出结果如下，

Rotation matrix Rz: (0.707107 -0.707107 0 0.707107 0.707107 0 0 0 1)
local x-axis: (0.707107 0.707107 0)
local y-axis: (-0.707107 0.707107 0)
local z-axis: (0 0 1)

以上代码实现的功能其实也很好理解：如果我知道局部坐标的 $e_3$ (或者 $z$ ) 方向是 $(0,0,1)$ , 局部坐标的 $e_1$ (或者 $x$ ) 方向是 $(1,1,0)$ , 如何得到旋转矩阵 $R_z$ , 以及局部的基向量。

算例2

有些时候我们并不关心局部坐标中的 $x$ 方向，比如复合材料的注射，有时只是区分层间和面内。我们可不可以指定一个 $z$ 轴方向，然后乱写一个局部的 $x$ 方向呢？其实是可以的。在算例1的代码中，e3_local 和 e1_local 是正交的，但其不正交也能运行，比如下面的代码，

#include "fvCFD.H"
#include "axesRotation.H"
int main(int argc, char *argv[])
{
    vector e3_local (1,1,2);
    vector e1_local (0,1,0); //e1 is clearly not orthogonal to e3.
    tensor R_mat = axesRotation(e3_local, e1_local).R();
    vector local_e1 = axesRotation(e3_local, e1_local).e1();
    vector local_e2 = axesRotation(e3_local, e1_local).e2();
    vector local_e3 = axesRotation(e3_local, e1_local).e3();
    Info << "Rotation matrix RxRyRz: " << R_mat << nl;
    Info << "local x-axis: " << local_e1 << nl;
    Info << "local y-axis: " << local_e2 << nl;
    Info << "local z-axis: " << local_e3 << nl;
    return 0;
}

输出如下，

Rotation matrix RxRyRz: (-0.182574 -0.894427 0.408248 0.912871 0 0.408248 -0.365148 0.447214 0.816497)
local x-axis: (-0.182574 0.912871 -0.365148)
local y-axis: (-0.894427 0 0.447214)
local z-axis: (0.408248 0.408248 0.816497)

看来OpenFOAM可以自己确定一个局部的 $x$ 方向。

算例3

有了以上两个例子，我们可以开始操作张量了。假设我们有一个复合材料， $K_x=K_y=10^{-10}\ m^2$ , $K_z=10^{-11}\ m^2$ . 我们知道局部的 $z$ 轴方向 $(1,1,2)$ , 如何确定局部的 $K$ 张量？把我们的测试求解器改成如下的代码，

#include "fvCFD.H"
#include "axesRotation.H"
int main(int argc, char *argv[])
{
vector e3_local (1,1,2), e1_local (0.1,1,0.59); //e1 is clearly not orthogonal to e3. It is a random vector.
scalar Kxy (1e-10), Kz (1e-11);
tensor K_ori (Kxy, 0, 0, 0, Kxy, 0, 0, 0, Kz); //permeability tensor in original frame
tensor R_mat = axesRotation(e3_local, e1_local).R(); //rotation matrix
tensor K_loc = R_mat & K_ori & R_mat.T(); //local permeability tensor 
Info << "Rotation matrix RxRyRz: " << R_mat << nl;
Info << "Local K tensor: " << K_loc << nl;
return 0;
}

再次编译并运行，打印坐标变换矩阵和局部渗透率张量，

Rotation matrix RxRyRz: (-0.399308 -0.820906 0.408248 0.884182 -0.227059 0.408248 -0.242437 0.523982 0.816497)
Local K tensor: (8.5e-11 -1.5e-11 -3e-11 -1.5e-11 8.5e-11 -3e-11 -3e-11 -3e-11 4e-11)

也就是说在OpenFOAM里面如果知道一个cell的局部 $z$ 轴方向，就可以快速的求出局部的渗透率张量。

算例4

补充一个对向量进行变换的例子。在原始坐标系下有个向量 $(1,1,1)$ ，变换到某个以 $(1,0.5,2)$ 为 $z$ 轴, $(0,1,-0.25)$ 为 $x$ 轴的局部坐标系中，求出变换后的坐标，有如下代码，

#include "fvCFD.H"
#include "axesRotation.H"
int main(int argc, char *argv[])
{
    vector e3_local (1,0.5,2), e1_local (0,1,-0.25), vec (1,1,1);  
    tensor R_mat = axesRotation(e3_local, e1_local).R(); 
    vector vec_loc = R_mat & vec; // local vecctor
    vector local_e1 = axesRotation(e3_local, e1_local).e1();
    vector local_e2 = axesRotation(e3_local, e1_local).e2();
    vector local_e3 = axesRotation(e3_local, e1_local).e3();
    Info << "Rotation matrix RxRyRz: " << R_mat << nl;
    Info << "Local vec: " << vec_loc << nl;
    Info << "local x-axis: " << local_e1 << nl;
    Info << "local y-axis: " << local_e2 << nl;
    Info << "local z-axis: " << local_e3 << nl;
    return 0;
}

输出如下，

Rotation matrix RxRyRz: (0 -0.899735 0.436436 0.970143 0.105851 0.218218 -0.242536 0.423405 0.872872)
Local vec: (-0.4633 1.29421 1.05374)
local x-axis: (0 0.970143 -0.242536)
local y-axis: (-0.899735 0.105851 0.423405)
local z-axis: (0.436436 0.218218 0.872872)

算例5

既然前面浅浅的铺垫了一些变换坐标的方法，那我们不如自己造个算例模拟一下试一试。以下所使用求解器是根据Horgue et al.的开源代码修改而来。我们可以让求解器读取每一个cell的nz和nx，即局部的 $x$ 方向和 $z$ 方向，只读就行了，写就不必了，

volVectorField nz
(
    IOobject
    (
    "nz",
    runTime.constant(),
    mesh,
    IOobject::MUST_READ,
    IOobject::NO_WRITE
    ), mesh
);

volVectorField nx
(
    IOobject
    (
    "nx",
    runTime.constant(),
    mesh,
    IOobject::MUST_READ,
    IOobject::NO_WRITE
    ), mesh
);

然后插入计算渗透率的代码，

for (int cellI = 0; cellI < mesh.C().size(); cellI++)
{
    R_mat = axesRotation(nz[cellI], nx[cellI]).R();
    K[cellI] = R_mat & K[cellI] & R_mat.T();    
}
runTime.write();

下面自己造个网格，下图是个四分之一的圆管，在中间的位置有一个小的圆形区域进行了网格的加密，原始的 $xyz$ 方向在左下角。对于每一个cell来说，局部的 $z$ 方向就是cell中心的x坐标，y坐标，0。用OF的语言就是，

for (int cellI = 0; cellI < mesh.C().size(); cellI++)
{
    nz[cellI]=mesh.C()[cellI];
    nz[cellI][2] = 0 ;
}

局部的 $x$ 方向就先指定 $(0,0,1)$ 。渗透率的话， $K_x=10^{-10}\ m^2$ ， $K_y=5\times 10^{-11}\ m^2$ , $K_z=10^{-11}\ m^2$ ，这样注射应该能在上面看到一个椭圆。至于注入的压强，设置一个合理的数值即可。

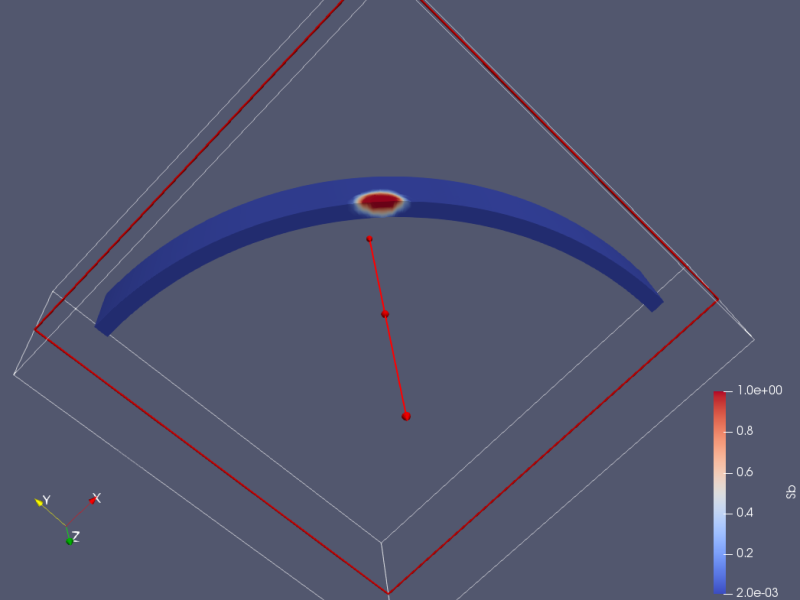
模拟结果，在15s时的填充效果，红色区域代表已填充，蓝色代表未注射，

如果把它切开，可以看到 $z$ 方向上的填充速度是要比另外两个方向慢的，

OpenFOAM中的坐标变换

算例1

算例2

算例3

算例4

算例5

pyqtgraph绘图窗口嵌入PyQt5界面

[OpenFOAM] 编程基础 06 Custom Classes

Comments NOTHING

取消回复