Please refresh the page if equations are not rendered correctly.
---------------------------------------------------------------
第二章 随机变量及其分布
定义 随机变量 设随机试验的样本空间为 S= \lbrace e \rbrace. X=X(e) 是定义在样本空间 S 上 的实值单值函数. 称 X=X(e) 为随机变量.
与函数类比:
- 样本空间 \rightarrow 函数的定义域
- 样本e \rightarrow 函数的自变量
- 实值单值函数X \rightarrow 函数关系
- 随机变量 \rightarrow 函数值与函数的区别:
- 随机变量的取值随试验的结果而定,在试验之前不能预知它取什么值,
- 且它的取值有一定的概率.这些性质显示了随机变量与普通函数有着本质的差异.
离散型随机变量及其分布律
定义 离散型随机变量 全部可能取到的值是有限个或可列无限多个的随机变量
设离散型随机变量 X 所有可能取的值为 x_{k}(k=1,2, \cdots), X 取各个可能值的概率, 即事件\lbrace X=x_{k} \rbrace 的概率, 为
P \lbrace X=x_{k} \rbrace = p_{k}, k=1,2, \cdots .
由概率的定义, p_{k} 满足如下两个条件:
\begin{aligned}
& 1^{\circ} \quad p_{k} \geqslant 0, k=1,2, \cdots ; \\
& 2^{\circ} \sum_{k=1}^{\infty} p_{k}=1 . \\
\end{aligned}
2^{\circ} 是由于 \lbrace X=x_{1} \rbrace \bigcup \lbrace X=x_{2} \rbrace \cup \cdots 是必然事件, 且 \lbrace X=x_{j} \rbrace \cap \lbrace X=x_{k} \rbrace
= \varnothing, k \neq j,故 1=P \left[ \bigcup_{k=1}^{\infty} \lbrace X=x_{k} \rbrace \right]=\sum_{k=1}^{\infty} P \lbrace X=x_{k} \rbrace \text {, 即 } \sum_{k=1}^{\infty} p_{k}=1.
(0 - 1)分布
设随机变量 X 只可能取 0 与 1 两个值, 它的分布律是
P\lbrace X = k \rbrace = p^{k}(1-p)^{1-k}, k = 0,1 \quad (0<p<1),
则称 X 服从以 p 为参数的 (0-1) 分布或两点分布. 其中p是取值为1的概率。
伯努利试验、二顶分布X \sim b(n,p)
设试验 E 只有两个可能结果: A 及 \bar{A}, 则称 E 为伯努利 (Bernoulli)试验. 设 P(A)=p(0<p<1), 此时 P(\bar{A})=1-p. 将 E 独立重复地进行 n 次, 则称这 一串重复的独立试验为 n 重伯努利试验。这里“重复”是指在每次试验中 P(A)=p保持不变; “独立”是指各次试验的结果互不影响(放回抽样)。
由于各次试验是相互独立的, 因此事件 A 在指定的 k(0 \leqslant k \leqslant n) 次试验中发生, 在其他 n-k 次试验中 A 不发生(例如在前 k 次试验中 A发生,而后n-k次试验中A不发生)的概率为
\underbrace{p \cdot p \cdot \cdots \cdot p}_{k \uparrow} \cdot \underbrace{(1-p) \cdot(1-p) \cdot \cdots \cdot(1-p)}_{n-k \text { 个 }}=p^{k}(1-p)^{n-k} .
这种指定的方式共有 \left(\begin{array}{l}n \ k\end{array}\right) 种, 它们是两两互不相容的, 故在 n 次试验中 A 发生 k 次 的概率为\left(\begin{array}{l}n \\ k\end{array}\right) p^{k}(1-p)^{n-k}, 记 q=1-p, 即有
P \lbrace X=k \rbrace =\left(\begin{array}{l}
n \\
k \end{array}\right) p^{k} q^{n-k}, k=0,1,2, \cdots, n .
当n = 1 时二项分布化为(0 - 1) 分布。
泊松分布
设随机变量 X 所有可能取的值为 0,1,2, \cdots, 而取各个值的概率为
P \lbrace X = k \rbrace = \frac{ \lambda^{ k } \mathrm{ e }^{- \lambda }} {k !}, k=0,1,2, \cdots,
其中 \lambda>0 是常数. 则称 X 服从参数为 \lambda 的泊松分布, 记为 X \sim \pi(\lambda).
以n,p为参数的二项分布的概率值可以由参数为\lambda = np 的泊松分布的概率值近似.
泊松定理 设 \lambda>0 是一个常数, n 是任意正整数, 设 n p_{n}=\lambda, 则对于任一固 定的非负整数 k,有
\lim _{n \rightarrow \infty} \left(\begin{array}{l}
n \\\ k \end{array}\right) p_{n}^{k}\left(1-p_{n}\right)^{n-k}=\frac{\lambda^{k} \mathrm{e}^{-\lambda}}{k !}一般, 当 n \geqslant 20, p \leqslant 0.05 时用\frac{\lambda^{k} \mathrm{e}^{-\lambda}}{k !}(\lambda= n p)作为 \left(\begin{array}{l}n \ k\end{array}\right) p^{k}(1-p)^{n-k}的近似值效果颇佳.
随机变量的分布函数
随机变量所取的值落在一个区间 \left(x_{1}, x_{2}\right] 的概率: P\lbrace x_{1}<X \leqslant x_{2} \rbrace:
P \lbrace x_{1}<X \leqslant x_{2} \rbrace =P \lbrace X \leqslant x_{2} \rbrace -P \lbrace X \leqslant x_{1} \rbrace,
定义 设 X 是一个随机变量, x 是任意实数,函数
F(x)=P \lbrace X \leqslant x \rbrace,-\infty<x<\infty
称为 X 的分布函数.
F(x)是取值在区间[0,1]的不减函数。
连续型随机变量的概率密度及其分布
对于随机变量 X 的分布函数 F(x), 存在非负函数 f(x), 使对于任意实数 x 有
F(x)=\int_{-\infty}^{x} f(t) \mathrm{d} t,
则称 X 为连续型随机变量,其中函数 f(x) 称为 X 的概率密度函数, 简称概率密度。连续型随机变量的分布函数是连续函数. 在实际应用中遇到的基本上是离散型或连续型随机变量。由定义知道,概率密度 f(x) 具有以下性质:
1^{\circ} f(x) \geqslant 0;
2^{\circ} \int_{-\infty}^{\infty} f(x) \mathrm{d} x=1;
3^{\circ} 对于任意实数 x_{1}, x_{2}\left(x_{1} \leqslant x_{2}\right),
P \lbrace x_{1}<X \leqslant x_{2} \rbrace =F\left(x_{2}\right)-F\left(x_{1}\right)=\int_{-x_{1}}^{x_{2}} f(x) \mathrm{d} x,
4^{\circ} 若 f(x) 在点 x 处连续, 则有 F^{\prime}(x)=f(x).
概率密度的定义与物理学中的线密度的定义相类似, 这就是为什么称f位)为概率密度的缘故.
若不计高阶无穷小,有: P \lbrace x< X \leq x+ \Delta x \approx f(x) \Delta x \rbrace
均匀分布 X \sim U(a,b)
若连续型随机变量 \mid X 具有概率密度
f(x)= \begin{cases}\frac{1}{b-a},&a<x<b, \ 0,&\text { 其他, }\end{cases}
称 X 在区间 (a, b) 上服从均匀分布. 记为 X \sim U(a, b).

概率密度函数下方的总面积为1,因为面积代表概率,而概率是必须为1。
指数分布
若连续型随机变量 X 的概率密度为
f(x)= \begin{cases}\frac{1}{\beta} \mathrm{e}^{-x / \beta},&x>0, \ 0,&\text { 其他, }\end{cases}
其中 \theta>0 为常数, 则称 X 服从参数为 \theta 的指数分布.
累积分布函数为:
F(x ; \beta)=\lbrace \begin{array}{cl}
1-e^{- \frac{1}{\beta} x}&, x > 0 \\
0&, x<0
\end{array} .


无记忆性特点需要理解
正态分布/高斯分布X \sim N\left(\mu, \sigma^{2}\right)
若连续型随机变量 X 的概率密度为
f(x)=\frac{1}{\sqrt{2 \pi \sigma}} \mathrm{e}^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}},-\infty<x<\infty,
其中 \mu, \sigma(\sigma>0) 为常数, 则称 X 服从参数为 \mu, \sigma 的正态分布或高斯 (Gauss) 分布, 记为 X \sim N\left(\mu, \sigma^{2}\right).
特别, 当 \mu=0, \sigma=1 时称随机变量 X 服从标准正态分布. 其概率密度和分 布函数分别用 \varphi(x), \Phi(x) 表示, 即有
\begin{gathered}
\varphi(x)=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-t^{2} / 2}, \\
\Phi(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} \mathrm{e}^{-t^{2} / 2} \mathrm{~d} t .
\end{gathered}
其中:
\Phi(-x) = 1-\Phi(x)
一般, 若 X \sim N\left(\mu, \sigma^{2}\right), 我们只要通过一个线性变换就能将它化成标准正态 分布.
引理 若 X \sim N\left(\mu, \sigma^{2}\right), 则 Z=\frac{X-\mu}{\sigma} \sim N(0,1).


Comments 1 条评论
正态分布中“\sigma原则”、“2\sigma原则”、“3\sigma原则”分别是:
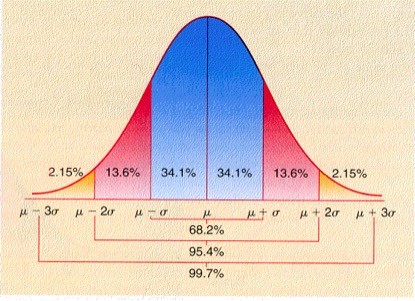
\sigma原则:数值分布在(μ-σ,μ+σ)中的概率为0.6826;
2\sigma原则:数值分布在(μ-2σ,μ+2σ)中的概率为0.9544;
3\sigma原则:数值分布在(μ-3σ,μ+3σ)中的概率为0.9974;