Please refresh the page if equations are not rendered correctly.
---------------------------------------------------------------

复合材料学报

Acta Materiae Compositae Sinica                    ISSN 1000-3851 CN 11-1801/TB

---

DOI:10.13801/j.cnki.fhclxb.20230427.001

织物增强复合材料Micro-CT辅助数值仿真技术研究进展

杨斌^{1,2}，王继辉^1，冯雨薇^1，杨超^1，倪爱清^{3*}

（1. 武汉理工大学 材料科学与工程学院 武汉 430070；2. Polytechnique Montreal, Department of Mechanical Engineering, Montreal H3T 1J4; 3. 武汉理工大学 材料复合新技术国家重点实验室，武汉 430070；）

摘 要：精确的数值模型是获得可靠的数值仿真结果的前提。显微计算机断层扫描（Micro-CT）技术可无损成像复合材料的内部结构，据此建立的数值模型比理想化模型更具代表性。本文综述了基于Micro-CT图像的复合材料介观模型构建方法及其在材料虚拟测试中的应用，提出了Micro-CT辅助数值仿真的概念。首先，对Micro-CT成像原理、设备特点和织物增强复合材料的成像难点进行了讨论。其次，梳理了现有的Micro-CT辅助建模技术的特点，将其建立的模型划分为间接模型、体素模型和数字材料孪生模型，重点介绍了构建各类模型的理论基础和技术途径，指出了各自的优势和局限性。然后对Micro-CT辅助数值仿真技术在织物增强复合材料的成型工艺和力学性能预测等方面的应用进行了总结，表明了该技术的重要价值。最后，对Micro-CT辅助数值仿真技术的未来发展进行了展望。

关键词：织物增强复合材料；Micro-CT；数值模型；图像重建；数字孪生

中图分类号：TB332 文献标识码：A

Advances in Micro-CT aided numerical simulation of fabric-reinforced composites

YANG Bin^{1,2}, WANG Jihui^1, FENG Yuwei^1, YANG Chao^1, NI Aiqing^{3*}

(1. School of Materials Science and Engineering, Wuhan University of Technology, Wuhan 430070, China；2. Polytechnique Montreal, Department of Mechanical Engineering, Montreal H3T 1J4, Canada; 3. State Key Laboratory of Advanced Technology for Materials Synthesis and Processing, Wuhan University of Technology, Wuhan 430070, China)

Abstract: Reliable numerical simulation results depend on the use of accurate numerical models. Micro-computed tomography (Micro-CT) technology is capable of non-destructively imaging the internal structure of composite materials, hence, numerical models reconstructed from it are more representative than the idealized ones. Here, a review is presented for constructing mesoscopic models of composite materials based on Micro-CT images and its application in virtual testing. A novel concept, Micro-CT aided numerical simulation, is proposed. First, the principle of Micro-CT imaging, the characteristics of equipment, and the difficulties with scanning fabric-reinforced composites are discussed. Second, the characteristics of existing Micro-CT aided modeling techniques are analyzed and compared. The models are divided into three types including indirect, voxel, and digital material twin ones. The theoretical basis and technical approaches for constructing each type of model are highlighted, and the advantages and limitations of each are analyzed. Then recent applications of Micro-CT aided numerical simulation in composite molding process and mechanical property prediction of fabric reinforced composites are summarized, showing the potential and importance of the technology. Finally, the future of Micro-CT aided numerical simulation technology is anticipated.

Keywords: fabric-reinforced composites; Micro-CT; numerical simulation; image reconstruction; digital twin

  数值仿真技术是织物增强复合材料结构和工艺设计的重要手段。近年来，以数值仿真技术为基础，发展出了复合材料虚拟测试[1]、高通量计算[2]和数字孪生[3,4]等现代化复合材料表征和设计手段。织物增强复合材料具有结构多尺度、增强材料显著各向异性等特点。研究表明，增强织物的微观和介观结构对织物工艺性能和复合材料宏观性质有显著影响[5,6]。因此，建立具有代表性的多尺度数值模型，尤其是连接微观和宏观尺度的复合材料介观单胞模型，对提高数值仿真技术准确性具有重要意义。

  织物增强复合材料介观单胞模型的传统建模方法根据理论基础可以分为以模拟织物几何形貌为主要目的的简化理想模型，和基于基本力学原理预测和构建复合材料介观结构的介观建模。前者以诺丁汉大学开发的TexGen[7,8]建模软件为代表，通过分别定义纤维束中心路径和横截面形状来定义增强织物的几何形状，并分别使用三次样条曲线和理想二维形状（如椭圆、长方形和透镜状等）来对中心路径和纤维束截面形状进行参数化表示[9]。此外，基于通用CAD或有限元软件建立介观单胞模型也是常用方法之一[10-15]，其途径与TexGen基本一致。

  基于基本力学原理的建模软件以天主教鲁汶大学开发的WiseTex[16,17]最为著名，通过数值仿真预测纤维或纤维束在编织过程中可能发生的压缩、弯曲和拉伸等状态变化来确定织物的介观形貌。类似的建模方法还见于金天国等[18]、Stump等[19]和Wadekar等[20]的工作中。这两类模型都可以用来快速预测织物及其复合材料的性能。然而，以上两类建模方法对织物结构进行的大量简化降低了仿真结果的准确性[21,22]。

  近年来，显微计算机断层扫描（X-ray Micro-Computed Tomography, Micro-CT）技术在复合材料的制造工艺设计([23])、缺陷形成[24]、力学行为和失效机制[25]等方面得到广泛应用。它以非侵入和无损的方式在较高的分辨率（400 纳米至70微米[26]）对复合材料的内部结构进行成像，避免了物理切片造成的样品损坏和污染。高精度扫描结果可以为研究人员提供样品内部的几何信息和结构信息，从而帮助了解样本的内部显微结构。根据数据获取目的的不同，Micro-CT的应用可以分为两类：

1) 形貌特征观测：通过Micro-CT三维成像获取试样的结构和形貌[27]（如尺寸、破坏形貌等）、组分分布和损伤扩展路径等，以解释介观和微观结构对材料力学性能、失效机制或制造缺陷的形成过程的影响，或用以验证理论和数值研究的结果。
2) Micro-CT辅助建模：将Micro-CT三维图像序列转化为可用于制造工艺和力学行为仿真的高精度数值模型[28]。由于三维图像仅包含标量信息，而织物增强复合材料各向异性和多尺度信息的表达需要将标量信息矢量化，为构建高效的Micro-CT辅助建模方法带来挑战。

  上述第一类应用发展较早，相关数据处理和分析手段已十分完备。Micro-CT辅助建模仍处在快速发展阶段，近10年来，研究人员报道了基于克里金插值[21]、结构张量法[29]、机器学习[30]等不同理论的辅助建模方法，显著提高了介观单胞模型的精度。然而，不同纺织工艺制备的织物增强材料在拓扑结构和几何形貌方面存在巨大差异，已有方法仍缺乏普适性。

  本文旨在总结介观尺度下Micro-CT辅助建模和数值仿真技术的国内外发展现状，梳理现有的技术途径和存在的问题，以期指出可行的发展方向和解决方案。本文对Micro-CT的成像原理和设备特点、织物复合材料成像的难点和解决措施、基于Micro-CT图像的辅助建模技术和在织物增强材料的工艺性能和复合材料的力学性能预测等方面的应用进行了详细的分析和讨论。根据技术路径将Micro-CT建模技术分为间接辅助建模和直接辅助建模两类，并讨论了各自的特点和局限性。最后，针对织物增强复合材料Micro-CT辅助数值仿真技术仍存在的问题和未来发展趋势进行了总结和展望。

1. 纤维织物增强复合材料的多尺度结构

  与颗粒增强复合材料[31,32]和短纤维增强复合材料[33,34]不同，连续纤维织物增强复合材料具有复杂的多尺度结构。如图 1所示，增强织物由大量的纤维束编织而成，每根纤维束又包含几百到几千根纤维单丝。纤维束之间存在毫米尺度的介观空隙，而纤维束中单丝之间的微观空隙则处于微米尺度。后者在体积上比介观空隙小约两个数量级。

  纤维织物的介观和微观结构会随着织物预成型、成型模具闭合和树脂浸渍压力梯度变化等工艺过程不断变化。增强织物压实程度的增加会导致多尺度孔隙网络的形态同时发生两种变化：一是纤维束中的纤维重排，导致微孔体积减小；二是纤维束重排，导致介观空隙体积减小。同时，在介观和微观尺度上，压实改变了增强材料的比表面积、介观/微观孔隙网络的迂曲度和纤维体积含量分布。

图 1 织物增强复合材料多尺度结构
Fig. 1 Multi-scale structure of textile reinforcements

(a) Formation of voids due to non-uniform velocity field[35]

(b) Non-uniform axial (left) and transverse (right) strain fields [36]

图 2 增强织物多尺度结构对复合材料加工和力学性能的影响
Fig. 2 Effect of multi-scale structure on manufacturing process and mechanical properties of composites

1.1 多尺度结构对成型质量的影响

  织物的多尺度结构对成型质量的影响主要表现为制品中的孔隙缺陷[37]。纤维织物增强材料的多尺度结构导致了渗透率[38]的空间变化，造成纤维束间和束内树脂浸渍速度不一致[39,40]。如图 2(a)所示，当纤维束间的树脂流动速度低于纤维束内时，空气会被困在纤维束之间，形成介观孔隙。与之相反，当纤维束间的树脂流动速度高于纤维束内时，气泡更容易被纤维束包裹，形成微观孔隙。此外，纤维束内流体承受的阻力远大于束间，因此树脂一旦进入纤维束内几乎被“固定”，而束间的树脂尚可随着灌注过程的进行而流动，导致纤维束内和束间的树脂固化周期不一致，产生残余应力[41,42]。

1.2 多尺度结构对力学行为的影响

  多尺度各向异性复合材料内部的应力场具有高度非均匀化的特点，应力和应变分布对织物的编织结构具有显著依赖性[36,43]。图 2(b)给出了通过数值仿真获得的二维三轴织物承受横向拉伸载荷时的应变云图。两者都显示出显著的自由边缘效应，即应力/应变集中沿纤维束自由边缘周期性地分布[36])。因此，使用能够准确反映织物或复合材料细观结构的介观模型进行力学性能预测和损伤失效分析对提高复合材料结构设计的可靠性具有重要意义。

2. 显微计算机断层扫描成像技术概述

2.1 成像原理

  典型Micro-CT设备包括X射线发生器、试样台、出射X射线束探测器和一台安装了射线信息重建和图像处理软件包的计算机。X射线从发生器发出，通过被检测试样并与试样发生光电吸收或/和康普顿散射[44]作用而出现光强度衰减。单色X射线束通过均质材料的衰减程度遵循Lambert-Beer定律[45]：
I_{x} = I_{0}e^{- \mu x} \tag{1}其中，I_{0}是X射线束的初始光强度。I_{x} 是射线在被测材料内部传播距离x\ (m)而发生衰减后的射线强度。\mu是线性衰减系数(m^{- 1})，统计学上等于光子平均自由程（Mean Free Path, MFP）的倒数，即射线光子在与被测物质的分子发生相互作用之前在其内部经过的路程的统计平均距离的倒数。当入射X射线能量较低时（~100 - 150 keV），光电吸收是最主要的衰减机制，随着X射线束能量的升高，康普顿散射逐步占据主导地位[46]。线性衰减系数\mu与射线能量E、被测物质的原子系数Z_{e}和密度\rho有如下关系[47]：
\mu(E) = \rho\left( a(E)Z_{e}^{3.8} + b(E) \right) \tag{2}表明光电效应与被测物质的原子序数Z_{e}呈指数关系（式(2) 右侧第1项），而康普顿散射与Z_{e}成正比（式(2)右侧第2项）。因此，低能量的X射线对多组分试样的组分界面更敏感，但衰减速度快，穿透能力低，只能用于小尺寸试样的测试。

  与被测试样作用后的出射X射线束的强度和强度空间分布信息可以通过射线探测器转换为电荷，以灰度图像像素矩阵的方式存储，称为射线照片（radiographs）。或者使用闪烁体探测器将出射X射线束转换为可见光，然后利用电荷耦合器件（Charged-Coupled Devices, CCD）作为图像传感器捕捉记录可见光信息。以给定步长在180°或360°范围内旋转试样台（或探测器和X射线源）获取一系列不同方向的射线照片，便可以使用适当的算法（例如滤波反投影算法[48]和代数重建技术[49]）将射线照片重建为2D图像序列（或3D体积图像）。

2.2 同步辐射和锥形束计算机断层扫描成像技术

  图 3展示了两种最常用的Micro-CT的成像原理。它们包含的组件相似，区别仅在于由X射线光源发出的射线束的几何形状不同。如图 3所示，同步辐射计算机断层扫描仪采用具有特定X射线能量（波长）的平行单色X射线束作为入射光源。成像分辨率与光源到待测样品的距离无关。对于均质材料，由于同步辐射光源的单色性，方程 (1)可直接用于X射线衰减曲线的计算，从而重建物质的内部结构影像。然而，纤维增强复合材料通常是由多个具有不同衰减系数的材料组分构成的，因此，方程(1)演变为：
I_{x} = I_{0}e^{- \sum_{i = 0}^{N}\mu_{i}x} \tag{3}其中i代表复合材料中的第i个材料组分。
  锥形束计算机断层扫描仪则采用锥形束X射线作为成像光源。它产生的X射线束是由不同能量（波长）的光子组成的锥形光束。因此，射线与被测试样作用后的衰减程度不仅取决于试样材料，还与入射光束的能量E的分布有关。因此，计算锥形束射线通过被测试样的能量损失时，射线的能量分布以积分的形式表示[50,51]：
I_{x} = \int I_{0}(E)e^{- \sum_{i =0}^{N}\mu_{i}x_{i}}dE \tag{4}  同步辐射计算机断层扫描技术使用平行单色X射线成像，具有更高的分辨率（可达数十纳米）、更小的信噪比、更高的光谱亮度和成像效率[52,53]。然而，同步辐射光源产生的射线能量一般较低（ 35 keV），穿透能力弱，无法成像厚度较大的材料，设备和操作成本也高于锥形束计算机断层扫描仪。因此，后者在研究中的应用更为普遍。目前，锥形束计算机断层扫描仪的扫描分辨率可以达到亚微米级。

图 3 显微计算机断层扫描成像的x射线源：同步辐射光源（上）和锥形束光源（下）

Fig. 3 Imaging of microcomputed tomography: X-ray beam initiates from synchrotron light sources (top) and from cone-beam source (bottom)

  计算机断层扫描成像技术的局限性在于相似组分成像对比度低，且成像分辨率和试样体积呈负相关的关系。例如，由于碳纤维与聚合物基体的密度接近，Micro-CT成像对比度低的问题在碳纤维复合材料成像时相比玻璃纤维复合材料更为突出[54]。由方程(2)可知，降低辐射电压产生较低能量的入射X射线束可以提高相似组分的成像对比度。然而，为达到足够高的成像亮度，通常需要延长辐照时间，容易诱发离焦辐射（off-focus radiation），导致成像质量降低[26,55]。此外，还必须确保X射线束的能量足够高以能够穿透样品，同时不能过高，以尽量减少对试样的热损伤。因此，根据试样的组分和体积确定最佳的辐射强度对高质量成像至关重要。Garcea等[46], Wielhorski 等[52], 和Rashidi 等[54]对这两个问题进行了更详细的讨论。目前已发表的文献鲜有给出完善的扫描参数，多注重于扫描图像数据的处理和分析[56,57]。考虑到复合材料的可设计性和复杂性，单一机构难以完成材料性质-扫描参数-成像质量关系的数据库的构建。因此，发表研究成果时，完整描述扫描参数和材料性质对Micro-CT技术的进一步推广应用具有重要意义。

2.3 Micro-CT辅助数值仿真技术

  Micro-CT辅助数值仿真是指利用Micro-CT获取的三维图像建立材料的数值模型，并以此为基础进行制造工艺和力学性能仿真的技术途径。它包含Micro-CT辅助建模和数值仿真两个部分。其中，Micro-CT辅助建模是Micro-CT辅助数值仿真技术的关键。

  当前已存在大量用于Micro-CT三维图像可视化、预处理（降噪、平滑等）和非均质材料模型重构的商业或开源软件，如Simpleware[58]，Materialise Mimics[59]，VGStudio[60]，3D Slicer[61]和Avizo[62]等，在医学和岩石物理等领域已经得到广泛应用。然而，为建立基于Micro CT辅助技术的织物增强复合材料精细化介观数值模型，还需要解决以下挑战：

  (1) 束间界面识别：增强织物的经纱、纬纱等纱线根据织物组织形式按一定规律形成浮沉交织的结构。纱线的交点处必然出现相互穿插和嵌套的现象，形成了介观尺度下Micro-CT难以分辨的同种材质界面。如图 4(a) - (c)所示，已有软件可以较为容易的分割和重建具有明显边界的纤维束，然而对于图 4(d)所示的纤维束界面则难以处理。

  (2) 微观空隙分布：纤维单丝间微米级的微观空隙决定了单胞内微观纤维体积含量的空间分布，对于评估织物的渗流性能和力学性能及复合材料的微观应力分析至关重要。然而，由于 Micro-CT的成像分辨率与试样尺寸负相关。为了得到完整的织物单胞结构，成像分辨率一般要大于10微米，因此无法观测到微观空隙的分布。

  (3) 标量数据矢量化：Micro-CT只输出标量信息，而纤维的空间取向对显著各向异性织物复合材料的数值仿真是必不可少的信息，因此将标量数据矢量化然后赋值给数值模型也是Micro-CT辅助建模的重要挑战之一。

图 4 图像分割与重建

Fig. 4 Image segmentation and reconstruction

  这些挑战也是研究人员重点关注的课题[21,63-65]。据作者所知，当前尚不存在可以完美解决以上问题的自动化解决方案，仍需要大量的人力介入才能够实现基于图像的织物复合材料精细化介观模型构建。

3. Micro-CT辅助建模

  根据对Micro-CT三维图像利用方式的不同，本文将Micro-CT辅助建模技术分为两类：

  (1) 间接建模技术：通过Micro-CT测量增强织物的几何形貌和尺寸信息，将测试数据输入到几何建模软件（如TexGen等）中构建复合材料介观模型；

  (2) 直接建模技术：通过将Micro-CT图像中各组分进行分割后，根据其空间分布信息对感兴趣的区域（Region Of Interest, ROI）直接进行离散，生成织物的介观模型。该类模型又可分为体素模型和数字材料孪生模型。

3.1 间接建模技术

  间接建模技术的优势在于不需要复杂的图像处理知识，只需要确定几何建模软件所需要的参数，然后使用基础的图像处理软件（如开源软件ImageJ[66]）从三维图像中测量获取，最后输入到几何建模软件中获得织物或复合材料的简化模型。这些参数一般包括织物的编织类型、纤维束的宽度、高度和纤维束间距等。纤维束的走向通过指定关键点并选择合适的插值方法来确定（见图 5a）。截面则可以采用指定的规则或不规则几何形状来近似（见图 5b）。

图 5 间接建模技术的纤维束路径、轮廓特征定义和尺寸数据分析[67]
Fig. 5 Fiber yarn paths, profile definition and dimensional analysis for indirect modeling techniques [67]

  为充分利用Micro-CT获取的大量数据，提高模型准确性，统计学方法在间接建模技术中被广泛使用。Yu等[67])对平纹织物Micro-CT图像中的纱线横截面分别用圆和椭圆拟合来测量纱线的长、宽和横截面积的变化，计算了横截面内的纤维体积含量，发现纬纱和经纱在交叉点相互挤压时纤维束内纤维体积分数V_{f}升高，两者分离时则反之，并统计分析了这些参量的变化趋势和离散度（图 5c）。Liu等[65]从Micro-CT图像中提取了三维五向编织复合材料中的纤维束几何特征参数，建立了该织物的简化模型和统计模型。实验结果显示基于统计修正模型的数值分析的精度要优于简化模型。Tao等[68,69]统计发现3D正交织物的纤维束的宽度和高度呈负相关，且纤维束截面积随着远离经纱和纬纱的交叉点而增大，这一结果与Yu等[67]的报道一致。作者使用统计结果在TexGen中建立了该织物复合材料的介观数值模型，并预测了材料的力学性能。曹欣怡等[70]，王童童[71]，Isart 等[72]和Zeng等[7,22,73]也报道了类似工作。

3.2 直接建模技术

  织物增强复合材料介观结构的直接建模技术一般包含图 6所示的步骤，即图像降噪和平滑，相组分分割、结构的空间差异性分析和区域离散。其中，图像的降噪、平滑和相组分割属于预处理过程，为构建介观模型提供输入数据。结构的空间差异性分析则是为了获取描述复合材料各向异性和非均质特征的基本数据，最终赋值给通过区域离散得到的有限元模型，用于数值分析。通常直接建模技术可以根据应用需求调控所建立模型的精度。当不满足要求时，需要重新检视以上各个步骤，调整相关建模参数，直到满足模型精度要求。

  直接建模技术需要对三维图像进行大量操作，需要人员具备图像处理、数值离散和计算机编程等相关知识背景。而且，第2.3节总结的与复合材料微结构密切相关的技术难点使得直接建模技术更具挑战性。然而，通过直接建模技术构建的模型的精度要远远优于间接建模技术构建的理想模型，可以显著改善数值仿真的结果精度[74-76]，因此成为近年来的研究热点。通过文献梳理，本文又将使用直接建模技术构建的介观模型分为体素模型和数字材料孪生模型两种。本节详细讨论了这两种模型的构建方法和各自的特点。

图 6 织物结构直接建模技术流程图
Fig. 6 Flow chart of direct textile geometrical modeling technique

3.2.1 Micro-CT图像预处理

  半影、伪影和噪声[77,78]是Micro-CT图像最可能出现的质量缺陷。伪影是由于X射线光源的焦点并非理想点光源，实际具有一定尺寸（<100微米）造成的。射线光源尺寸越小，半影对成像质量的影响越弱。因此，尽可能的选用尺寸更小的光源是消除半影的根本办法[78]。伪影也与Micro-CT设备有关，可以采用伪影校正等图像处理手段消除[79]。噪声(noise)是在图像获取时传感器受随机信号干扰产生的像素亮度随机变化的孤立像素点。噪声与要研究的对象性质无关，但是会影响图像分析结果，需要使用空域滤波器（中值滤波器、均值滤波器、高斯滤波器等）、频域滤波器（傅里叶变换、余弦变换等）或数学形态学图像处理操作（腐蚀和膨胀等）等方法消除。钱浩[78]发现中值滤波器既可以消除噪声，又可以保留较为清晰的纤维束-纤维束和纤维束-基体界面。而高斯滤波虽然同样能达到去除噪声的效果，不同组分间的界面也变得模糊。图像分割依赖于纤维束间界面的锐度，纤维束内部细节特征并不关注，因此选取中值滤波对图像进行预处理。

  图像分割是形貌分析和将三维图像直接转化为数值模型的基础，它将由Micro-CT产生的复合材料三位图像序列分割成多个图像目标，即基体和纤维织物，并定位图像中目标的边界和目标之间的界面。每一组具有特定特征的体素都被赋予特定标签，即复合材料中的基体或纤维束。图像分割技术可以分为三类：手工分割、传统分割（如阈值分割等）和机器学习分割算法[6,30,80]。其中，手工分割常常被用作测试基准，来评估后两者的精度。

  织物增强复合材料的方向性特点使得Micro-CT图像也存在相应的灰度梯度，因此，用于分析图像灰度梯度信息的结构张量法也常常被用于Micro-CT图像分割[74,76,81]。该方法利用图像I沿图像水平（x轴）和垂直（y轴）方向的偏导数f_{x}和f_{y}在每一个像素点i构建结构张量S_{i}:

  然后对结构张量进行特征值分解获得特征和特征向量，其中特征向量表示梯度方向，而特征值则表明了沿其相应特征向量方向的梯度的确定性（强弱程度）。对于三维图像，结构张量扩展为：

  与二维结构张量一样，也可以通过特征值分解确定像素的方向性。目前为止，结构张量法是最实用的方法，对低纤维体积含量的织物分割显示出良好的鲁棒性。然而，在高纤维体积含量的试样中，不仅纤维束间界面无法清晰成像，图像的灰度梯度也变得不再显著，结构张量法需要结合其他图像分析工具共同完成图像分割任务[74,76]。表 1总结了部分文献中常用的图像预处理和分割方法和软件。

表 1 Micro-CT 图像预处理和图像分割方法
Table 1 Micro-CT image pre-processing and image segmentation methods

Textile	Resolution/μm	Denosing	Smoothing	Segmentation	Software	Reference
Plain weave	10.4	/	/	Manual segmentation	VG studio	[67]
25	Pixel intensity averaged with neighbors	Sobel operator & Structure tensor	MATLAB	[77]
1 - 10	Median filter	Threshold-texture feature-morphology	/	[78]
5	A 1D uniform filter	Morphological gradient & Deep Learning	ImageJ & SciPy	[82]
18.6	Non-local mean filter	thresholding based on seed region growing	Avizo	[83]
5-directional braided composite	22.1	√	√	√	VG studio/ImageJ	[65]
Fiber tow	9.3	/	Nugget effect	Implicit kriging & Indicator function	In-house Python code	[84]
3D fabric	2	Median filter	Texture analysis	/	[74]
/	Gaussian smoothing	Structure tensor & Signed distances	MATLAB	[64]

Note: “/” means information of the item was not given by authors, while “√” means the item was done but the method was not given.

3.2.2 体素模型

  体素模型是指采用大量规则、均匀的体素（立方体）的有序组合来表示三维实体的模型。基于体素模型的数值求解器通常内存需求更少，求解速度更快[85]。通过Micro-CT获取的三维图像本身就是一个体素模型（对应于二维图片的像素），每个体素对应的灰度值代表了不同的组分。因此，一般体素模型不需要额外的算法来生成。只需要利用图像分割算法将三维图像中的体素进行分类，即可获得三种不同的模型(见图 7)：复合材料的体素模型[81]、基体的体素模型[23,86]或者增强织物的体素模型[74,77,87]。

  体素模型最初主要用于计算流体力学分析[88]。目前，在复合材料力学行为分析中的应用也越来越多[81,86]。即使如此，在选用体素模型时仍然需要充分它的考虑以下缺点[64,89]：（1）基体和增强材料的界面是阶梯状的（如图 7a所示），可能在界面的某些点上产生人为的高应力区[90]，因此不适合用于材料失效有关的数值仿真。（2）模型中体素的大小一般是均匀的，表达相同的模型细节要比自适应有限元网格需要更多的单元数。（3）使用较为粗大的体素单元也可能使全局的纤维体积分数不再与实际一致。

3.2.3 数字材料孪生模型

  织物增强复合材料的数字材料孪生模型（Digital Material Twin, DMT）的概念首先由Huang等 [21]提出。本质上，数字材料孪生模型是满足以下条件的复合材料详细形态描述：

  (1) 考虑了材料结构和性质的空间离散性。

  (2) 准确性可以根据扫描样本的分辨率进行评估，并根据建模需要调整。

  (3) 可用于数据驱动的数值模拟，以预测复合材料的力学性能或织物的工艺特性。

  构建数字材料孪生模型的本质是将一个包含多根纤维束和基体等子域的多材料空间进行离散，界面两侧的子域共享节点，保证界面的单元边和节点能完全重合且平滑，即形成共形网格。因此，确定各个子域的边界面是关键。根据构建边界面策略大致可分为显式和隐式界面重建方法[91]。

图 7 织物增强复合材料体素模型
Fig. 7 Voxel model for fabric-reinforced composites

  显式表面重建方法以构成表面轮廓的点云数据为输入，因此需要在对图像进行分割后提取每一个子域的表面点云，创建的曲面网格的顶点基本上都是输入的点云的一部分，从而最大程度地保持重建网格和输入点云几何特征的一致性。常用的显式表面重建方法有参数化曲面[6,21]和三角化表面[62,92]，其中以Kriging法[93]为基础的纤维束表面参数化曲面重建方法的研究报道最为常见[6,21,27,84,94-96]。如图 8a所示的纤维束的轮廓曲面，其上的点可以使用参数s和t表示：

  则纤维束的轮廓曲面的向量形式的参数方程可以表示为：
\mathbf{r}(s,t) = x(s,t)\mathbf{i} + y(s,t)\mathbf{j} + z(s,t)\mathbf{k}
  根据参数Kriging法[38]的定义，x(s,t), y(s,t)和z(s,t)可以表达为如下形式：
\mathbf{w}\mathbf{(}t,s\mathbf{) =}\mathbf{k}_{\mathbf{1}}\mathbf{(}t\mathbf{) \cdot}\mathbf{T}^{\mathbf{- 1}}\mathbf{\cdot}\mathbf{P}_{\mathbf{w}}\mathbf{(}t,s\mathbf{) \cdot}\mathbf{S}^{\mathbf{- 1}}\mathbf{\cdot}\mathbf{k}_{\mathbf{2}}\mathbf{(}s\mathbf{)}^{\mathbf{T}}\mathbf{,\ \ }w = x,y,z
其中，P_{w}是由坐标分量构成的矩阵，以x为例，P_{x}可表示为：

k_t(s)和k_2(s)是两个向量，S和T为矩阵。它们的具形式均与基函数的选取有关。以二次函数为基函数为例，k_{1}(t)和k_{2}(s)具有如下形式：

  S和T可以表示为：

K_{1}\left( \left| t_{i} - t_{j} \right| \right)和K_{2}\left( \left| s_{i} - s_{j} \right| \right)是两点之间距离的函数，具体的形式可以根据需要选择。图 8b和图 8c分别展示了使用Kriging方法重建后的曲面和引入块金效应平滑后的曲面。作者与Micro-CT图像对比发现采用该方法重建的曲面可以较好的保留织物结构的细节。Huang等[21]在此基础上提出了一系列评估重建精度的方法。需要注意的是，显式算法重构的曲面质量与输入的点云数据的质量密切相关，因此图像预处理非常关键。隐式表面重建方法通过标量函数场的等值面来表达需要重建的表面。最大优点是能够生成一个平滑水密的曲面[91,97]。其步骤是首先生成一个函数的标量场（如有符号距离函数），然后提取该标量场的等值面作为子域的表面。可以通过选用不同的场函数，或对场函数进行平滑操作，使产生的等值面具有理想的平滑度。Wintiba等[64]获取了图 9(a)所示的3D正交织物的Micro-CT图像：包含8根经纱，6根纬纱和2根束缚纱。作者使用MATLAB内嵌函数alphaShape对纤维束进行了分割，建立了各个纤维束内的点到纤维束表面的有符号距离场（signed distance fields），然后采用水平集法提取了如图 9(b)所示的纤维束表面作为基体-纤维束和纤维束-纤维束间的界面。最后，采用Kamel等[98]提出的多材料共形网格离散方法建立了如图 9(c)所示的多尺度介观共形网格。在隐式表面重建方法中，除了使用有符号距离场作为标量函数场外，Madra等[84]直接采用Micro-CT图像的灰度值和使用深度学习构建的图像分割概率场作为标量函数场，采用隐式Kriging法提取纤维束表面，不再需要构建额外的标量场。然而该方法需要图像具有较高的分辨率，对于常见的分辨率低于10nm的Micro-CT扫描结果适用性较差。

  无论采用显式还是隐式重建方法，一旦各个子域的表面重构完成，可以选择将其离散为三角曲面网格[62,92]，然后使用四面体单元填充表面网格来生成体网格得到三维数值仿真模型。此外，也可以以重构界面为边界，使用开源网格划分软件TetGen[99]或同类软件直接将计算域进行离散，生成多材料共形网格[64,74]。网格单元的取向根据纤维的走向确定[89,100]。

4. Micro-CT辅助数值仿真技术的应用

  图 10(a)以“Micro-CT/Micro-Computed tomography & composite”为关键词分析了Micro-CT在研究复合材料相关问题时中的使用频次随年份的变化关系（数据于2022年6月5日从Engineering Village检索获取）。结果表明，Micro-CT越来越多地被用于研究介观和微观尺度的复合材料相关的科学问题：2003年仅6篇被SCI索引的科技文献使用了Micro-CT作为表征手段，随后逐年增长，2018年之后，这一数字增长到超过300篇/年。

图 8 基于Kriging的显式参数化表面重建方法[6]
Fig. 8 Kriging-based explicit parametric surface reconstruction method

图 9 隐式表面重建方法生成的共形网格[64]
Fig. 9 Conformal mesh generated by implicit surface reconstruction method

图 10 采用显微计算机断层扫描技术研究复合材料的历年文献发表数量
Fig. 10 Number of scientific literatures applying micro tomography in investigations

  分别用关键词“manufacturing process”、“mechanical behavior”和“defect”进一步对文献分析发现（图 10(b)），Micro-CT早期主要用作表征复合材料内部缺陷的无损成像工具。近十年来，它在复合材料力学行为和制造工艺等方面研究上的应用取得了巨大的发展。其中，以Micro-CT图像为基础的直接建模技术应用较为广泛，其生成的数字孪生模型可以准确描述织物的形貌，作为数值仿真的输入，在优化复合材料的制造工艺和结构设计等方面具有良好的应用前景。如图 11所示，围绕数字孪生模型，不仅可以构建基于数字预成型体的织物铺放和渗透性能的虚拟测试，还可以建立数字复合材料虚拟测试和设计途径。两者结合，实现以虚拟数字手段构建织物复合材料的“组分性质-复合结构-成型工艺-使用性能”的关系图谱。

图 11 复合材料数字孪生技术应用图谱
Fig. 11 Application of digital twin technology for composite materials

  正如图 10所示，有关Micro-CT辅助数值仿真技术的应用的相关文献数目繁多，本文在有限的篇幅内仅总结了与增强织物渗透率、悬垂性和复合材料力学性能的虚拟测试相关的代表性文献。如果有近年来发表的相关专题的综述，本文将以参考文献的形式给出，方便感兴趣的读者查阅。

4.1 渗透率

  渗透率是增强织物允许流体通过的能力的度量，是复合材料成型工艺设计需要的重要参数。实验法测试渗透率成本高、耗时耗力却难以得到准确结果，相关的测试尚无标准可依[101-103]。因此，基于Micro-CT图像的增强织物渗透率虚拟测试[100,104]方法在近五年逐渐发展起来。由于纤维束内孔隙对织物整体的渗透性影响很小（一般小于10%），基于Micro-CT图像的虚拟渗透率测试常将纤维束视为不可渗透的固体，即忽略微观层次结构如纤维束内孔隙及其分布特点对整体渗透能力的影响[5,105,106]，只考虑纤维束之间介观空隙对流体的输运能力。在此前提下，渗透率的预测可以从求解微观-介观双尺度的流动问题简化为求解介观尺度的流动问题。考虑到复合材料成型时，树脂在增强织物中的流速较低（雷诺数Re<1），与黏性力相比，惯性力可以忽略，因此数值仿真选用的控制方程通常为Stokes方程：

其中，\mathbf{u}, p和\mu分别是流体的速度、压力和黏度。通过求解上述方程，即可得到织物单胞模型内的压力、速度分布云图（如图 12 (b)和(c)所示）和通过求解域的流体体积流速Q_{V}（m³/s），根据达西定律可知织物在求解方向的渗透率K：
K=\frac{\mathfrak{\mu}{Q}_V}{\text{A }\nabla\text{p}}
  其中A为试样的横截面积（m²），\text{∇}\text{p}为施加的压力梯度（Pa/m）。图 12(a)给出了常用的边界条件施加方式：在进口和出口处施加压力边界，产生压力梯度\text{∇}\text{p}驱使流体从入口向出口流动，其他边界一般选择施加无滑移边界条件。

  Ali M.A等[23,105,107,108]获取了三维正交机织物和角度联锁织物在不同纤维体积含量下的Micro-CT图像，基于该图像分析了纱线及束间孔隙大小分布以及孔隙变形情况，重构了织物单胞的介观尺度体素模型用于预测渗透率。研究结果表明织物渗透率随织物内部几何变化表现出一定的空间变异性。曹鹏军等[109]基于Micro-CT图像构建了五枚缎纹织物的体素模型，通过对多组扫描结果的分析也确认了织物渗透率具有一定的空间离散性的特点。其基于图像预测的渗透率均值为1.18×10⁻¹² m²，与实验值（1.25×10⁻¹² m²）吻合较好。通过对Micro-CT图像的深入分析，作者还发现织物渗透率的大小受织物束间孔隙率、孔隙曲折程度、以及孔隙连通性影响，即孔隙连通性好、孔隙率大且孔隙迂曲程度小的织物渗透性较高。

(a) Boundary conditions
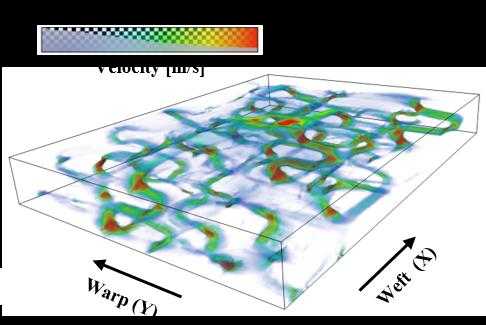(b) Velocity fields

图 12 基于体素模型的渗透率预测：(a) 边界条件和(b)速度云图[109]
Fig. 12 Permeability prediction based on voxel model[109]

  表2给出了可以用于虚拟渗透率测试的常用多孔介质渗流力学求解器及其求解的控制方程和所依赖的网格类型。目前为止，经典的计算流体力学求解器（表 2中第一类和第三类）在虚拟渗透率测试中仍占据主流。Lattice-Boltzmann (LBM)方法具有计算效率高、易于编程实现，并且可以直接在体素网格上进行的计算，非常适用于解决复杂形状计算域中的流体力学问题，因此常被用来研究孔隙尺度的多孔介质的流动，在渗透率的虚拟测试方面有较好的应用前景。

表 2 五种常用的多孔介质渗流力学求解器
Table 2 Five commonly used solvers for percolation mechanics in porous media

Category	Governing equation	Meshing	software	Reference
Computational Fluid Dynamic (CFD)	Stokes and Navier-Stokes equations on discretized grid mesh	Yes	Fluent, OpenFOAM, et al,	[92,110,111]
Lattice-Boltzmann Method (LBM)	Boltzmann equation on voxel mesh	No	OpenLB et al.	[112,113]
Voxel Based direct Navier-Stokes Solvers (VBS)	Stokes and Navier-Stokes equations on segmented Micro-CT images	No	VG studio, Avizo et al.	[73,105,107,109,114]
Semi-Analytical Solvers (SAS)	Analytical up-scaling solutions	No	/	[115]
Empirical Kozeny–Carman type model (EMP)	pore size distribution extracted from	No	/	[5,88]

4.2 织物悬垂性

  织物的悬垂性（Drapability）是描述纺织材料在自然悬垂状态下因自重下垂形成平滑曲面的性能指标。在织物增强复合材料领域，常常用来描述增强织物的预成型性能[83]，如织物的压缩性[116]、剪切性[75]和模具的贴合性，对增强织物的工艺性能和其制备的复合材料力学性能有重要影响[74,76]。选用具有优异的悬垂性的织物作为增强材料可以有效的减少预成型过程中织物的起皱、纤维束弯曲和扭曲等缺陷[117]的产生， 对具有复杂几何外形的复合材料构件尤其重要。

  Micro-CT的使用使获取织物在预成型过程中的形貌变化成为可能。Huang等[95,96]使用Micro-CT获取了平纹织物在纤维体积分数为47.6%、50.8%、55.0%三种情况下的三维图像，并使用基于Kriging的显式重建方法生成了相应的数字材料孪生模型，使得能够分析织物在不同压缩程度下的形貌变化。形貌分析表明在压缩过程中，纤维束在垂直压缩方向上具有明显的位移，横向位移则几乎可以忽略。Chen等[118]发现织物的嵌套和层间滑移是引起同种织物预成型体的压缩性具有一定离散性的主要原因。Naouar等[74]使用基于Micro-CT图像构建的数字材料孪生模型模拟了3D正交织物的压缩性能，结果表明该模型相比理想模型能够更好的反映织物的真实形貌，数值仿真获得织物压缩响应曲线与试验一致性较好。然而，这一方面基于数字材料孪生模型的研究目前还较少，方法的准确性、可靠性和普适性还需要进一步验证。

4.3 力学性能

  织物增强复合材料的力学性能，包括拉伸、压缩、弯曲和冲击等可能导致损伤和失效行为，一直都是科研和工程人员关注的重点。介观有限元模拟是研究编织复合材料复杂破坏行为（如压缩破坏[120]和冲击破坏[121, 122]的重要手段，能够较好地预测复合材料整体应力-应变响应，预测结果与实验表征之间具有较好的吻合性。在采用数值方法预测复合材料的损伤和失效行为时，首先需要确保选取合适的失效准则以预测损伤起始点及其发展过程（如Hashin准则[86]、Hoffman准则[119]和Puck准则[64]等）。其次，数值模型需要能够准确代表仿真对象的结构。Isart等[72]通过对比理想模型、数字单元法建立的模型和根据Micro-CT数据建立的模型发现，复合材料的弹性常数预测精度与模型的精度、尤其是纤维束截面形状的代表性密切相关。如图 13所示，理想化模型中纤维束的部分截面积与实际偏差超过20%，导致复合材料整体纤维体积含量比实际小7%、 弹性常数的预测结果与实验值的偏差超过10% [72]。数字单元法和根据Micro-CT数据建立的模型中的纤维束轮廓与CT图像吻合较好，全局纤维体积分数与实际值的偏差小于1%。采用后两者预测的复合材料弹性常数与实验值几乎一致。

  Liu等[86]对比了采用理想模型和基于Micro-CT图像的体素模型得到的复合材料损伤和失效仿真结果，发现与理想化的模型相比，体素模型的预测结果与实验结果的一致性更好。此外，实际中纤维束的不规则形状容易诱发损伤，因此，模型中纤维束形状的局部细节对复合材料弹性常数预测精度的影响较小，对损伤和失效的预测准确性起着关键作用。类似的报道还有[65]、[64]和[76]等，证实了Micro-CT辅助建模和仿真技术的重要性。

  在介观尺度的有限元模型中，合理的边界条件是必要的。它能够影响整体应力应变响应和变形模式以及局部损伤破坏特征[123]。并且，合理利用周期性边界条件能够减小模型的尺寸，有效提高计算效率[124]。基于理想周期性假设的复合材料介观模型在数值仿真中可以非常容易的施加周期性边界条件，用于模拟大尺寸材料或结构。然而，基于Micro-CT建立的介观模型一般不满足周期性假设。为解决这一问题，Akpoyomare等[124]基于插值算法改进了周期性边界施加方法。

图 13 不同精度的数值模型和X方向的拉伸应力云图[72]
Fig. 13 Numerical models with different accuracy and tensile stress field in x-direction[72]

5. 总结与展望

5.1 总结

  Micro-CT辅助数值模拟技术显著提高了织物增强复合材料成型工艺过程和力学性能数值预测的准确性。本文对基于Micro-CT图像的建模流程进行了深入讨论，包括成像原理、设备特点和织物复合材料的成像难点，并给出了解决方法。根据技术路径不同，对现有的Micro-CT辅助建模技术进行了梳理，将建立的基于Micro-CT图像的数值模型分为间接模型、体素模型和数字材料孪生模型三类，阐明了其背后的建模原理、技术路径和各自的局限性。值得注意的是，尽管间接模型的精度低于体素模型和数字材料孪生模型，然而它可以利用已有的成熟软件快速生成适用于各种仿真软件的数值模型，实现材料性能的快速预测。相比之下，体素模型和数字孪生模型的构建则要复杂的多。因此，实际应用中需要在建模复杂度和数值仿真精度之间权衡，根据仿真目的选用最合适的建模方法。最后，本文分析了Micro-CT辅助数值仿真技术在织物增强材料的工艺性能和复合材料的力学性能预测等方面的应用，指出了模型精度在确保数值仿真的有效性、正确性和可重复性方面的重要性。

5.2 展望

  作为一种具有高精度特点的新兴技术，织物增强复合材料Micro-CT辅助数值仿真技术在近年来获得了快速发展。根据本文对国内外研究现状的综述，以下问题仍亟需解决或将成为今后的重点研究方向：

  （1）自动化图像分割技术

  准确的图像分割是Micro-CT辅助建模的关键。当前虽然存在多种传统的图像分割算法或新兴的基于机器学习的算法，对于压实程度较高、纤维束界面模糊的三维图像仍需要大量的人工介入，导致数字孪生模型的建模周期甚至长达数周，难以应用于工程实际。引入前沿的计算机图形学技术，开展跨学科合作，是解决这一问题的可行方案。

  （2）普适性的建模方法

  目前Micro-CT辅助建模的方法虽然多种多样，但往往与织物的结构相关，或严重依赖三维图像的质量。因此，汲取各方法的优点，并将其融合，建立一种普适性的Micro-CT辅助建模方法将有助于推动Micro-CT辅助数值仿真技术在工程领域的应用。

  （3）工艺-力学性能联合多尺度仿真

  长期以来，复合材料的工艺和力学性能仿真都是分别进行的。然而，工艺仿真所获取的如制造缺陷的形成和分布、织物的形貌随工艺条件的发展必然对复合材料的力学性能产生重要影响。因此，将两者联合起来，在基于Micro-CT图像构建的高精度多尺度模型上进行数值仿真是优化复合材料制造工艺和力学性能的有效手段。

  （4）实时数字孪生系统的构建

  数字孪生是物理世界的镜像，随时间变化（即物理世界和数字世界的演化）是其题中应有之义。目前，对数字孪生模型的应用还停留在进行增强织物渗透率或复合材料力学性能的虚拟测试的阶段，与其物理实体之间尚未构成不断演化的镜像关系。这将是未来实现真正意义的数字孪生系统的重要发展方向。

参考文献：

[1] LLORCA J, GONZÁLEZ C, MOLINA-ALDAREGUÍA J M, et al.Multiscale modeling of composite materials: A roadmap towards virtual testing[J].Advanced Materials,2011, 23 (44): 5130-5147.

[2] HENNING F, KÄRGER L, DÖRR D, et al.Fast processing and continuous simulation of automotive structural composite components[J].Composites Science and Technology,2019, 171: 261-279.

[3] GRIEVES M, VICKERS J: Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems,Transdisciplinary perspectives on complex systems: Springer,2017: 85-113.

[4] 张霖.关于数字孪生的冷思考及其背后的建模和仿真技术[J].系统仿真学报,2020, 32 (4): 744.

ZHANG Lin. Cool thoughts on digital twins and modeling and simulation technologies behind[J]. Journal of System Simulation, 2020, 32 (4): 744 (in Chinese).

[5] ENDRUWEIT A, ZENG X, Matveev M, et al.Effect of yarn cross-sectional shape on resin flow through inter-yarn gaps in textile reinforcements[J].Composites Part A: Applied Science and Manufacturing,2018, 104: 139-150.

[6] MADRA A, BREITKOPF P, RASSINEUX A, et al.Image-based model reconstruction and meshing of woven reinforcements in composites[J].International Journal for Numerical Methods in Engineering,2017, 112 (9): 1235-1252.

[7] ZENG X, ENDRUWEIT A, BROWN L P, et al.Numerical prediction of in-plane permeability for multilayer woven fabrics with manufacture-induced deformation[J].Composites Part A: Applied Science and Manufacturing,2015, 77: 266-274.

[8] LONG A C, BROWN L P: Modelling the geometry of textile reinforcements for composites: TexGen, Boisse P,editor,Composite Reinforcements for Optimum Performance: Woodhead Publishing,2011: 239-264.

[9] SHERBURN M. Geometric and mechanical modelling of textiles[D]. University of Nottingham Nottingham, UK,2007.

[10] WENDLING A, DANIEL J, HIVET G, et al.Meshing preprocessor for the Mesoscopic 3D finite element simulation of 2D and interlock fabric deformation[J].Applied Composite Materials,2015, 22 (6): 869-886.

[11] ISART N, MAYUGO J A, BLANCO N, et al.Geometric model for 3D through-thickness orthogonal interlock composites[J].Composite Structures,2015, 119: 787-798.

[12] 倪爱清, 王继辉, 朱以文.复合材料液体模塑成型工艺中预成型体渗透率张量的数值预测[J].复合材料学报,2007, 24 (6): 50-56.

NI Aiqing, WANG Jihui, ZHU Yiwen. Numerical prediction of saturated permeability tensor of a woven fabric for use in the fluid simulation of liquid composite molding[J]. Acta Materiae Compositae Sinica, 2007, 24(6): 50-56 (in Chinese).

[13] 王旭.基于3ds Max软件的机织物结构三维建模研究[J].安徽工程大学学报,2013, 28 (3): 4.

WANG Xu. 3D modeling on woven fabric structure by 3D Max[J]. Journal of Anhui Polytechnic University,2013, 28 (3): 4 (in Chinese).

[14] 惠新育, 许英杰, 张卫红, 等.平纹编织 SiC/SiC 复合材料多尺度建模及强度预测[J].复合材料学报,2019, 36 (10): 2380-2388.

HUI Xinyu, XU Yingjie, ZHANG Weihong, HE Zongbei. Multi-scale modeling and strength prediction of plain woven SiC/SiC composites[J]. Acta Materiae Compositae Sinica, 2019, 36(10): 2380-2388(in Chinese).

[15] YANG B, WANG S, TANG Q.Geometry modeling and permeability prediction for textile preforms with nesting in laminates[J].Polymer Composites,2018, 39 (12): 4408-4415.

[16] SWERY E E, MEIER R, LOMOV S V, et al.Predicting permeability based on flow simulations and textile modelling techniques: Comparison with experimental values and verification of FlowTex solver using Ansys CFX[J].Journal of Composite Materials,2016, 50 (5): 601-615.

[17] VERPOEST I, LOMOV S V.Virtual textile composites software WiseTex: Integration with micro-mechanical, permeability and structural analysis[J].Composites Science and Technology,2005, 65 (15-16): 2563-2574.

[18] 金天国, 魏雅君, 杨波, 等.预成型体渗透率预测及其受压缩变形的影响[J].复合材料学报,2015, 32 (3): 840-847.

JIN Tianguo, WEI Yajun, YANG Bo, BI Fengyang. Permeability prediction of preform and influence of compression deformation[J]. Acta Materiae Compositae Sinica, 2015, 32(3): 840-847 (in Chinese).

[19] STUMP D, FRASER W.A simplified model of fabric drape based on ring theory[J].Textile Research Journal,1996, 66 (8): 506-514.

[20] WADEKAR P, GOEL P, Amanatides C, et al.Geometric modeling of knitted fabrics using helicoid scaffolds[J].Journal of Engineered Fibers and Fabrics,2020, 15: 1558925020913871.

[21] HUANG W, CAUSSE P, Brailovski V, et al.Reconstruction of mesostructural material twin models of engineering textiles based on Micro-CT Aided Geometric Modeling[J].Composites Part A: Applied Science and Manufacturing,2019, 124 (June).

[22] ZENG X, BROWN L P, Endruweit A, et al.Geometrical modelling of 3D woven reinforcements for polymer composites: Prediction of fabric permeability and composite mechanical properties[J].Composites Part A: Applied Science and Manufacturing,2014, 56: 150-160.

[23] ALI M A, UMER R, KHAN K A.A virtual permeability measurement framework for fiber reinforcements using micro CT generated digital twins[J].International Journal of Lightweight Materials and Manufacture,2020, 3 (3): 204-216.

[24] BODAGHI M, LOMOV S V, SIMACEK P, et al.On the variability of permeability induced by reinforcement distortions and dual scale flow in liquid composite moulding: A review[J].Composites Part A: Applied Science and Manufacturing,2019, 120 (February): 188-210.

[25] GEREKE T, CHERIF C.A review of numerical models for 3D woven composite reinforcements[J].Composite Structures,2019, 209: 60-66.

[26] ORHAN K. Micro-computed Tomography (micro-CT) in Medicine and Engineering[M]. Springer,2020.

[27] MADRA A, CAUSSE P, Trochu F, et al.Stochastic characterization of textile reinforcements in composites based on X-ray microtomographic scans[J].Composite Structures,2019, 224: 111031.

[28] 许承海, 徐凯, 宋乐颖, 等.多向轴编碳/碳材料炭基体微结构 Micro-CT 原位扫描及其等效力[J].复合材料学报,2013, 1.

XU Chenghai, XU Kai, SONG Leying, et al. Microstructure characterization from X-ray micro-tomography and equivalent mechanical properties of carbon matrix of 4D in-plane carbon/carbon composites[J]. Acta Materiae Compositae Sinica, 2013, 1 (in Chinese).

[29] NGUYEN N Q, MEHDIKHANI M, STRAUMIT I, et al.Micro-CT measurement of fibre misalignment: Application to carbon/epoxy laminates manufactured in autoclave and by vacuum assisted resin transfer moulding[J].Composites Part A: Applied Science and Manufacturing,2018, 104: 14-23.

[30] ALI M A, GUAN Q, UMER R, et al.Efficient processing of μCT images using deep learning tools for generating digital material twins of woven fabrics[J].Composites Science and Technology,2022, 217: 109091.

[31] PENG P, GAO M, GUO E, et al.Deformation behavior and damage in B4Cp/6061Al composites: An actual 3D microstructure-based modeling[J].Materials Science and Engineering: A,2020, 781: 139169.

[32] WILLIAMS J, FLOM Z, AMELL A, et al.Damage evolution in SiC particle reinforced Al alloy matrix composites by X-ray synchrotron tomography[J].Acta Materialia,2010, 58 (18): 6194-6205.

[33] MADRA A, ADRIEN J, BREITKOPF P, et al.A clustering method for analysis of morphology of short natural fibers in composites based on X-ray microtomography[J].Composites Part A: Applied Science and Manufacturing,2017, 102: 184-195.

[34] AGYEI R F, SANGID M D.A supervised iterative approach to 3D microstructure reconstruction from acquired tomographic data of heterogeneous fibrous systems[J].Composite Structures,2018, 206: 234-246.

[35] HUANG W. Analysis of Through-Thickness Injection in Liquid Composite Molding Based on Digital Material Twins[D]. Polytechnique Montréal,2020.

[36] ZHANG C, LI N, WANG W, et al.Progressive damage simulation of triaxially braided composite using a 3D meso-scale finite element model[J].Composite Structures,2015, 125: 104-116.

[37] PATIÑO I D, POWER H, NIETO-LONDOÑO C, et al.Stokes–Brinkman formulation for prediction of void formation in dual-scale fibrous reinforcements: a BEM/DR-BEM simulation[J].Computational Mechanics,2017, 59 (4): 555-577.

[38] YANG B, HUANG W, CAUSSE P, et al.On the design of test molds based on unidirectional saturated flows to measure transverse permeability in liquid composite molding[J].Polymer Composites,2022.

[39] KANG M K, LEE W I, HAHN H T.Formation of microvoids during resin-transfer molding process[J].Composites Science and Technology,2000, 60 (12): 2427-2434.

[40] RUIZ E, ACHIM V, SOUKANE S, et al.Optimization of injection flow rate to minimize micro/macro-voids formation in resin transfer molded composites[J].Composites Science and Technology,2006, 66 (3-4): 475-486.

[41] YUAN Z, WANG Y, YANG G, et al.Evolution of curing residual stresses in composite using multi-scale method[J].Composites Part B: Engineering,2018, 155: 49-61.

[42] 王晓霞, 贾玉玺, 董抒华.基于 Morris 方法的纤维复合材料结构件固化均匀性的全局灵敏度分析[J].复合材料学报,2015, 32 (4): 1211-1217.

WANG Xiaoxia, JIA Yuxi, DONG Shuhua. Global sensitivity analysis of curing uniformity of fiber composite structures based on Morris method[J]. Acta Materiae Compositae Sinica, 2015, 32(4): 1211-1217 (in Chinese).

[43] 屈鹏. 纤维/树脂复合材料多尺度结构对力学性能的影响[D]. 济南: 山东大学,2012.

QU Peng. Influence of multiscale structure of fiber/resin composites on mechanical properties [D]. Jinan: Shandong University, 2012 (in Chinese).

[44] WELLINGTON S L, VINEGAR H J.X-ray computerized tomography[J].Journal of petroleum technology,1987, 39 (08): 885-898.

[45] MAYERHÖFER T G, PAHLOW S, POPP J.The Bouguer‐Beer‐Lambert Law: Shining Light on the Obscure[J].ChemPhysChem,2020, 21 (18): 2029-2046.

[46] GARCEA S C, WANG Y, Withers P J.X-ray computed tomography of polymer composites[J].Composites Science and Technology,2018, 156: 305-319.

[47] NIKISHKOV Y, AIROLDI L, MAKEEV A.Measurement of voids in composites by X-ray Computed Tomography[J].Composites Science and Technology,2013, 89: 89-97.

[48] FELDKAMP L A, DAVIS L C, Kress J W.Practical cone-beam algorithm[J].Journal of the Optical Society of America A,1984, 1 (6): 612.

[49] GORDON R, BENDER R, HERMAN G T.Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography[J].Journal of theoretical Biology,1970, 29 (3): 471-481.

[50] HAIDE R, FEST-SANTINI S, SANTINI M.Use of X-ray micro-computed tomography for the investigation of drying processes in porous media: A review[J].Drying Technology,2021: 1-14.

[51] ELBAKRI I A, FESSLER J A.Statistical image reconstruction for polyenergetic X-ray computed tomography[J].IEEE Transactions on Medical Imaging,2002, 21 (2): 89-99.

[52] WIELHORSKI Y, MENDOZA A, Rubino M, et al.Numerical modeling of 3D woven composite reinforcements: A review[J].Composites Part A: Applied Science and Manufacturing,2022, 154: 106729.

[53] GAO Y, HU W, XIN S, et al.A review of applications of CT imaging on fiber reinforced composites[J].Journal of Composite Materials,2022, 56 (1): 133-164.

[54] RASHIDI A, OLFATBAKHSH T, CRAWFORD B, et al.A Review of Current Challenges and Case Study toward Optimizing Micro-Computed X-Ray Tomography of Carbon Fabric Composites[J].Materials,2020, 13 (16): 3606.

[55] FLAY N, BROWN S, SUN W, et al.Effects of off-focal radiation on dimensional measurements in industrial cone-beam micro-focus X-ray computed tomography systems[J].Precision Engineering,2020, 66: 472-481.

[56] HE P, ZHAO W, YANG B, et al.Void content reduction of composites with sensor-aided injection strategy in liquid composite molding process[J].Materials Research Express,2021, 8 (7): 075309.

[57] MADRA A, HAJJ N E, BENZEGGAGH M.X-ray microtomography applications for quantitative and qualitative analysis of porosity in woven glass fiber reinforced thermoplastic[J].Composites Science and Technology,2014, 95: 50-58.

[58] ALIYEVA S, ALABBAD A, DAZA J P, et al. Elasticity, Electrical Conductivity and Permeability in Digital Rocks: A Comparative Study Using Simpleware, NIST, Comsol Multiphysics and Lattice-Boltzmann Algorithms[C].51st US Rock Mechanics/Geomechanics Symposium,2017.

[59] MILAN J-L, PLANELL J A, Lacroix D.Computational modelling of the mechanical environment of osteogenesis within a polylactic acid–calcium phosphate glass scaffold[J].Biomaterials,2009, 30 (25): 4219-4226.

[60] ZHANG Y, WANG Q.Application of software VGStudio MAX 2.0 in 3D reconstruction of industrial computed tomography images[J].Metrology & Measurement Technology,2011, 5.

[61] KIKINIS R, PIEPER S D, Vosburgh K G. 3D Slicer: a platform for subject-specific image analysis, visualization, and clinical support[M]. Springer,2014: 277-289.

[62] BIRD M B, BUTLER S L, HAWKES C D, et al.Numerical modeling of fluid and electrical currents through geometries based on synchrotron X-ray tomographic images of reservoir rocks using Avizo and COMSOL[J].Computers & Geosciences,2014, 73: 6-16.

[63] RASSINEUX A.Robust conformal adaptive meshing of complex textile composites unit cells[J].Composite Structures,2022, 279: 114740.

[64] WINTIBA B, VASIUKOV D, Panier S, et al.Automated reconstruction and conformal discretization of 3D woven composite CT scans with local fiber volume fraction control[J].Composite Structures,2020, 248: 112438.

[65] LIU X, ZHANG D, SUN J, et al.Refine reconstruction and verification of meso-scale modeling of three-dimensional five-directional braided composites from X-ray computed tomography data[J].Composite Structures,2020, 245: 112347.

[66] ABRÀMOFF M D, MAGALHÃES P J, Ram S J.Image processing with ImageJ[J].Biophotonics international,2004, 11 (7): 36-42.

[67] YU X-W, WANG H, WANG Z-W.Analysis of yarn fiber volume fraction in textile composites using scanning electron microscopy and X-ray micro-computed tomography[J].Journal of Reinforced Plastics and Composites,2018, 38 (5): 199-210.

[68] TAO W, ZHU P, XU C, et al.Uncertainty quantification of mechanical properties for three-dimensional orthogonal woven composites. Part II: Multiscale simulation[J].Composite Structures,2020, 235: 111764.

[69] TAO W, P, Xu C, et al.Uncertainty quantification of mechanical ZHU properties for three-dimensional orthogonal woven composites. Part I: Stochastic reinforcement geometry reconstruction[J].Composite Structures,2020, 235: 111763.

[70] 曹欣怡, 彭秀钟, 范进, 等.一种改进的基于两单胞模型的三维角联锁机织复合材料弹性性能数值预测方法及实验验证[J].复合材料学报,2021, 38 (11): 3718.

Xinyi CAO, Xiuzhong PENG, Jin FAN, Mengjing ZHOU. An improved numerical prediction method of elastic properties based on two unit-cells models for 3D angle-interlock woven composites and experimental verification[J]. Acta Materiae Compositae Sinica, 2021, 38(11): 3704-3713 (in Chinese).

[71] 王童童. 三维编织复合材料的制备及面内拉伸和剪切性能研究[D]. 哈尔滨工业大学,2019.

WANG Tongtong. The fabrication and in-plane tensile and shear performance of 3d woven composites [D]. Harbin Institute of Technology, 2019 (in Chinese).

[72] ISART N, EL SAID B, IVANOV D S, et al.Internal geometric modelling of 3D woven composites: A comparison between different approaches[J].Composite Structures,2015, 132: 1219-1230.

[73] AZIZ A R, ALI M A, ZENG X, et al.Transverse permeability of dry fiber preforms manufactured by automated fiber placement[J].Composites Science and Technology,2017, 152: 57-67.

[74] NAOUAR N, VIDAL-SALLE E, SCHNEIDER J, et al.3D composite reinforcement meso F.E. analyses based on X-ray computed tomography[J].Composite Structures,2015, 132: 1094-1104.

[75] IWATA A, INOUE T, NAOUAR N, et al.Coupled meso-macro simulation of woven fabric local deformation during draping[J].Composites Part A: Applied Science and Manufacturing,2019, 118 (January): 267-280.

[76] NAOUAR N, VASIUKOV D, PARK C H, et al.Meso-FE modelling of textile composites and X-ray tomography[J].Journal of Materials Science,2020, 55 (36): 16969-16989.

[77] WIJAYA W, ALI M A, UMER R, et al.An automatic methodology to CT-scans of 2D woven textile fabrics to structured finite element and voxel meshes[J].Composites Part A: Applied Science and Manufacturing,2019, 125: 105561.

[78] 钱浩. 平纹编织复合材料Micro CT成像试验与纤维束识别方法研究[D]. 国防科学技术大学, 2015.

QIAN Hao. Micro CT experiment and the method of yarn segmentation in plain-weave composites of Micro CT images[D]. National University of Defense Technology, 2015 (in Chinese).

[79] 宋永忠, 王俊山, 傅健.多向编织C/C复合材料显微结构的\mu-CT研究[J].宇航材料工艺,2011, 41 (2): 5.

SONG Yongzhong, WANG Junshan, FU Jian. Microstructure of 3D Carbon/Carbon Composites Measured With Micro-CT[J]. Aerospace Science and Technology,2011, 41 (2): 5 (in Chinese).

[80] BADRAN A, MARSHALL D, Legault Z, et al.Automated segmentation of computed tomography images of fiber-reinforced composites by deep learning[J].Journal of Materials Science,2020, 55 (34): 16273-16289.

[81] STRAUMIT I, LOMOV S V, WEVERS M.Quantification of the internal structure and automatic generation of voxel models of textile composites from X-ray computed tomography data[J].Composites Part A: Applied Science and Manufacturing,2015, 69: 150-158.

[82] SINCHUK Y, KIBLEUR P, AELTERMAN J, et al.Variational and Deep Learning Segmentation of Very-Low-Contrast X-ray Computed Tomography Images of Carbon/Epoxy Woven Composites[J].Materials,2020, 13 (4): 936.

[83] YOUSAF Z, WITHERS P J, POTLURI P.Compaction, nesting and image based permeability analysis of multi-layer dry preforms by computed tomography (CT)[J].Composite Structures,2021, 263: 113676.

[84] MADRA A, TROCHU F, BREITKOPF P. Implicit kriging model of fibrous reinforcements in composites based on X-ray microtomography[C].13e colloque national en calcul des structures,2017.

[85] SAXENA N, HOFMANN R, ALPAK F O, et al.References and benchmarks for pore-scale flow simulated using micro-CT images of porous media and digital rocks[J].Advances in Water Resources,2017, 109: 211-235.

[86] LIU Y, STRAUMIT I, VASIUKOV D, et al.Prediction of linear and non-linear behavior of 3D woven composite using mesoscopic voxel models reconstructed from X-ray micro-tomography[J].Composite Structures,2017, 179: 568-579.

[87] RINALDI R G, BLACKLOCK M, BALE H, et al.Generating virtual textile composite specimens using statistical data from micro-computed tomography: 3D tow representations[J].Journal of the Mechanics and Physics of Solids,2012, 60 (8): 1561-1581.

[88] ALI M A, UMER R, KHAN K A, et al.Application of X-ray computed tomography for the virtual permeability prediction of fiber reinforcements for liquid composite molding processes: A review[J].Composites Science and Technology,2019, 184 (September): 107828-107828.

[89] SINCHUK Y, PANNIER Y, ANTORANZ-GONZALEZ R, et al.Analysis of moisture diffusion induced stress in carbon/epoxy 3D textile composite materials with voids by µ-CT based Finite Element Models[J].Composite Structures,2019, 212: 561-570.

[90] DOITRAND A, FAGIANO C, IRISARRI F-X, et al.Comparison between voxel and consistent meso-scale models of woven composites[J].Composites Part A: Applied Science and Manufacturing,2015, 73: 143-154.

[91] NAGAI Y, OHTAKE Y, SUZUKI H.Tomographic surface reconstruction from point cloud[J].Computers & Graphics,2015, 46: 55-63.

[92] ZHAO Y, ZHU G, ZHANG C, et al.Pore-Scale Reconstruction and Simulation of Non-Darcy Flow in Synthetic Porous Rocks[J].Journal of Geophysical Research: Solid Earth,2018, 123 (4): 2770-2786.

[93] TROCHU F.A Contouring Program Based on Dual Kriging Interpolation[J].Engineering with Computers,1993, 9 (3): 160-177.

[94] MADRA A, BREITKOPF P, RAGHAVAN B, et al.Diffuse manifold learning of the geometry of woven reinforcements in composites[J].Comptes Rendus Mécanique,2018, 346 (7): 532-538.

[95] HUANG W, CAUSSE P, HU H, et al.Transverse compaction of 2D glass woven fabrics based on material twins - Part I: Geometric analysis[J].Composite Structures,2020, 237.

[96] HUANG W, CAUSSE P, HU H, et al.Transverse compaction of 2D glass woven fabrics based on material twins – Part II: Tow and fabric deformations[J].Composite Structures,2020, 237: 111963.

[97] BERGER M, TAGLIASACCHI A, SEVERSKY L, et al.State of the art in surface reconstruction from point clouds[J].Eurographics 2014-State of the Art Reports,2014, 1 (1): 161-185.

[98] EHAB MOUSTAFA KAMEL K, SONON B, MASSART T J.An integrated approach for the conformal discretization of complex inclusion-based microstructures[J].Computational Mechanics,2019, 64 (4): 1049-1071.

[99] SI H.TetGen, a Delaunay-based quality tetrahedral mesh generator[J].ACM Transactions on Mathematical Software (TOMS),2015, 41 (2): 1-36.

[100] SOLTANI P, JOHARI M S, ZARREBINI M.3D fiber orientation characterization of nonwoven fabrics using X-ray micro-computed tomography[J].World J Text Eng Technol,2015, 1: 41-47.

[101] ARBTER R, BERAUD J M, BINETRUY C, et al.Experimental determination of the permeability of textiles: A benchmark exercise[J].Composites Part A: Applied Science and Manufacturing,2011, 42 (9): 1157-1168.

[102] VERNET N, RUIZ E, ADVANI S, et al.Experimental determination of the permeability of engineering textiles: Benchmark II[J].Composites Part A: Applied Science and Manufacturing,2014, 61: 172-184.

[103] MAY D, AKTAS A, ADVANI S G, et al.In-plane permeability characterization of engineering textiles based on radial flow experiments : A benchmark exercise[J].Composites Part A: Applied Science and Manufacturing,2019, 121 (March): 100-114.

[104] SOLTANI P, JOHARI M S, ZARREBINI M.Effect of 3D fiber orientation on permeability of realistic fibrous porous networks[J].Powder Technology,2014, 254: 44-56.

[105] ALI M A, UMER R, KHAN K A, et al.Non-destructive evaluation of through-thickness permeability in 3D woven fabrics for composite fan blade applications[J].Aerospace Science and Technology,2018, 82-83 (October): 520-533.

[106] TAHIR M W, HALLSTRÖM S, ÅKERMO M.Effect of dual scale porosity on the overall permeability of fibrous structures[J].Composites science and technology,2014, 103: 56-62.

[107] ALI M A, UMER R, KHAN K A, et al.In-plane virtual permeability characterization of 3D woven fabrics using a hybrid experimental and numerical approach[J].Composites Science and Technology,2019, 173 (February): 99-109.

[108] ALI M A, UMER R, KHAN K A, et al.XCT-scan assisted flow path analysis and permeability prediction of a 3D woven fabric[J].Composites Part B: Engineering,2019, 176 (May): 107320-107320.

[109] 曹鹏军;赵文斌;杨斌;倪爱清;王继辉.基于Micro-CT图像的缎纹织物细观结构分析及渗透率预测[J].复合材料学报,2022, 40 (-): 1.

Pengjun CAO, Wenbin ZHAO, Bin YANG, Aiqing NI, Jihui WANG. Meso-structure analysis and permeability prediction of satin fabric based on Micro-CT[J]. Acta Materiae Compositae Sinica, 2022, 40 (-): 1(in Chinese).

[110] SOULAINE C, GJETVAJ F, GARING C, et al.The Impact of Sub-Resolution Porosity of X-ray Microtomography Images on the Permeability[J].Transport in Porous Media,2016, 113 (1): 227-243.

[111] RAEINI A Q, BIJELJIC B, BLUNT M J.Modelling capillary trapping using finite-volume simulation of two-phase flow directly on micro-CT images[J].Advances in Water Resources,2015, 83: 102-110.

[112] NABOVATI A, SOUSA A C M.Fluid flow simulation at open–porous medium interface using the lattice Boltzmann method[J].International Journal for Numerical Methods in Fluids,2008, 56 (8): 1449-1456.

[113] BELOV E B, LOMOV S V, VERPOEST I, et al.Modelling of permeability of textile reinforcements: lattice Boltzmann method[J].Composites Science and Technology,2004, 64 (7-8): 1069-1080.

[114] HUANG W, CAUSSE P, HU H, et al.Numerical and experimental investigation of saturated transverse permeability of 2D woven glass fabrics based on material twins[J].Polymer Composites,2020, 41 (4): 1341-1355.

[115] DONG H, BLUNT M J.Pore-network extraction from micro-computerized-tomography images[J].Physical Review E,2009, 80 (3): 036307.

[116] MAY D, AKTAS A, YONG A. International benchmark exercises of textile permeability and compressibility characterization[C].18th European Conference on Composite Materials,2018: 24-28.

[117] ZHU J, WANG J, ZU L.Influence of out-of-plane ply waviness on elastic properties of composite laminates under uniaxial loading[J].Composite Structures,2015, 132: 440-450.

[118] CHEN B, CHOU T-W.Compaction of woven-fabric preforms: nesting and multi-layer deformation[J].Composites Science and Technology,2000, 60 (12-13): 2223-2231.

[119] PAN Q.Multi-scale modelling and material characterisation of textile composites for aerospace applications[J],2016.

[120] 吕青泉, 赵振强, 李超, 等. 2.5D 机织复合材料的渐进损伤与失效模拟 [J]. 复合材料学报, 2021, 38(8): 2747-2757.

LV Qingquan, ZHAO Zhenqiang, LI Chao, et al. Progressive damage and failure simulation of 2.5D woven composites[J]. Acta Materiae Compositae Sinica, 2021, 38(8): 2747-2757(in Chinese).

[121] 曹勇, 张超. 薄层复合材料冲击损伤行为研究进展[J]. 航空学报, 2022, 43(6): 525323.

CAO Y, ZHANG C. Impact damage behavior of thin-ply composites: A review[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(6): 525323(in Chinese).

[122] ZHAO ZQ, LIU P, CHEN CY.Modeling the transverse tensile and compressive failure behavior of triaxially braided composite[J]. Composites Science and Technology, 2019, 172: 96-107.

[123] ZHAO ZQ, LIU P, DANG HY. Understanding the critical role of boundary conditions in meso‑scale finite element simulation of braided composites[J]. Advanced Composites and Hybrid Materials, 2022, 5: 39-49.

[124] AKPOYOMARE A I, OKEREKE M I, Bingley M S. Virtual testing of composites: Imposing periodic boundary conditions on general finite element meshes [J]. Composite Structures, 2017, 160: 983-994.